Δύναμη

Στη Φυσική δεχόμαστε ότι πάνω σε ένα σώμα μπορεί να επιδράσει κάποιο άλλο σώμα του περιβάλλοντος του. Στην ορολογία της Φυσικής, η επίδραση που δέχεται ένα σώμα από κάποιο άλλο, λέγεται δύναμη. Παραδείγματα δυνάμεων είναι η δύναμη του βάρους που ασκεί η Γη σε κάποιο σώμα. Η δύναμη του τεντωμένου ελατηρίου που ασκεί στο χέρι μας καθώς το τραβάμε. Η δύναμη που ασκεί η ρακέτα στο μπαλάκι καθώς το κτυπά.

Δύναμη και κίνηση

Ένας ποδοσφαιριστής για να στείλει στα δίκτυα την μπάλα, καθώς εκτελεί πέναλτι, κτυπά δυνατά την ακίνητη μπάλα με το πόδι του και αυτή φεύγει με ταχύτητα. Εδώ ο ποδοσφαιριστής ασκεί δύναμη με το πόδι του στην μπάλα για να μπορέσει να φύγει με ταχύτητα. Ο τερματοφύλακας αποκρούει την μπάλα με τα χέρια του αλλάζοντας την κατεύθυνση της ταχύτητας της μπάλας. Εδώ ο τερματοφύλακας ασκεί δύναμη με τα χέρια του στην μπάλα για να αλλάξει την κατεύθυνση της.

Εδώ βλέπουμε ότι η δύναμη προκαλεί αλλαγή της κινητικής κατάστασης του σώματος. Η μεταβολή της κινητικής κατάστασης ενός σώματος ή απλά μεταβολή της κίνησης του, εκδηλώνεται είτε ως μεταβολή του μέτρου της ταχύτητας που έχει, είτε ως μεταβολή της κατεύθυνσης της ή ταυτόχρονα και τα δυο.

Κάθε φορά που η ταχύτητα ενός σώματος αλλάζει (αλλάζει το μέτρο ή η κατεύθυνση ή και τα δυο) τότε συμπεραίνουμε ότι πάνω στο σώμα ασκείται δύναμη που προκαλεί αυτή τη μεταβολή.

Πρέπει να καταλάβουμε ότι για να αλλάξει η κινητική κατάσταση ενός σώματος μπορεί να γίνει μόνο όταν ασκηθεί στο σώμα η κατάλληλη δύναμη.

Συμπέρασμα: Οι δυνάμεις προκαλούν μεταβολή στην (στιγμιαία) ταχύτητα των σωμάτων πάνω στα οποία δρουν.

Δύναμη και παραμόρφωση

Μπορούμε να παραμορφώσουμε ένα αντικείμενο επιδρώντας σε αυτό, με αποτέλεσμα αυτό να αλλάζει σχήμα. Για παράδειγμα, με τα χέρια μας παραμορφώνουμε ένα κομμάτι πλαστελίνης, καθώς και όταν τραβώντας με το χέρι μας ένα ελατήριο το παραμορφώνουμε. Βλέπουμε εδώ, ότι η δύναμη που ασκούμε στο ελατήριο προκαλεί την παραμόρφωση του.

Συμπέρασμα: Οι δυνάμεις προκαλούν παραμόρφωση στα σώματα πάνω στα οποία ενεργούν.

Δυνάμεις και αλληλεπιδράσεις

Ένας ορισμός για την δύναμη μπορεί να είναι ο εξής: Δύναμη είναι το αίτιο που προκαλεί μεταβολή στην κινητική κατάσταση των σωμάτων ή την παραμόρφωση τους.

Όσο και να ψάξουμε δεν υπάρχει σώμα που μόνο να ασκεί δύναμη(εις) και σώμα που μόνο να δέχεται δύναμη(εις). Οι δυνάμεις εμφανίζονται ανά δύο μεταξύ των σωμάτων, δηλαδή τα σώματα αλληλοεπιδρούν μεταξύ τους.

Αυτό σημαίνει ότι αν ένα σώμα Α ασκεί μια δύναμη σε ένα άλλο σώμα Β τότε και το σώμα Β ασκεί δύναμη στο σώμα Α.

Παραδείγματα αλληλεπίδρασης σωμάτων. Ο ποδοσφαιριστής με το πόδι του ασκεί δύναμη στην μπάλα, όταν εκτελεί πέναλτι, αλλά και η μπάλα ασκεί δύναμη στο πόδι του ποδοσφαιριστή γι’ αυτό νιώθει πόνο. Ο Ήλιος ασκεί ελκτική δύναμη στη Γη και η Γη ασκεί ελκτική δύναμη στον Ήλιο.

Κατηγορίες δυνάμεων

Είπαμε ότι δύναμη είναι η επίδραση ενός σώματος σε ένα άλλο και ότι τα σώματα αλληλοεπιδρούν μεταξύ τους ασκώντας δύναμη το ένα το άλλο. Τα σώματα αυτά που αλληλοεπιδρούν μπορεί να βρίσκονται σε επαφή ή σε απόσταση. Έτσι ανάλογα με τον τρόπο αλληλεπίδρασης, οι δυνάμεις χωρίζονται σε δυο κατηγορίες:

Α. Δυνάμεις επαφής που δρουν όταν τα σώματα ασκούν δυνάμεις και είναι σε επαφή. Παραδείγματα δυνάμεων επαφής:
1] Οι δυνάμεις που ασκούν τα τεντωμένα σκοινιά ή τα ελατήρια σε σώματα που είναι δεμένα μαζί τους.
2] Οι δυνάμεις που ασκούνται μεταξύ σωμάτων που συγκρούονται.
3] Η δύναμη τριβής ανάμεσα σε δυο επιφάνειες που βρίσκονται σε επαφή.
4] Οι δυνάμεις που ασκούν τα υγρά στα τοιχώματα των δοχείων που βρίσκονται.

Β. Δυνάμεις από απόσταση δρουν όταν τα σώματα τα οποία ασκούν δυνάμεις, δεν είναι σε επαφή και βρίσκονται σε απόσταση μεταξύ τους. Παραδείγματα δυνάμεων από απόσταση:
1] Οι βαρυτικές δυνάμεις που ασκούνται μεταξύ των ουράνιων σωμάτων. Π.χ. η δύναμη που ασκεί ο Ήλιος στη Γη. Οι δυνάμεις βάρους που ασκεί η Γη σε σώματα που βρίσκονται στην επιφάνεια της ή σε κάποιο ύψος.
2] Οι ηλεκτρικές δυνάμεις που ασκούνται μεταξύ φορτισμένων σωμάτων.
3] Οι μαγνητικές δυνάμεις που ασκούνται μεταξύ μαγνητών και μεταξύ μαγνήτη και σιδερένιων αντικειμένων.

Μέτρηση της δύναμης

Η δύναμη είναι φυσικό μέγεθος διότι μπορεί να μετρηθεί. Για να μετρήσουμε μια δύναμη θα χρησιμοποιήσουμε τα αποτελέσματα που προκαλεί στα σώματα που δρα.

Γνωρίζουμε ότι η δύναμη που ασκείται σε ένα σώμα έχει ως αποτέλεσμα να μεταβάλει την ταχύτητα του. Μονάδα μέτρησης της Δύναμης στο Διεθνές Σύστημα Μονάδων είναι το 1Ν (Newton – Νιούτον). Δύναμη μέτρου 1Ν είναι η δύναμη που ασκείται σε ένα σώμα μάζας 1Kg και του μεταβάλει την ταχύτητα κατά 1m/s μέσα σε διάρκεια χρόνου 1s.

Έτσι για να μετράμε δυνάμεις θα μπορούσαμε να μετράμε μεταβολές της ταχύτητας του σώματος στο οποίο ενεργεί, αλλά αυτός ο τρόπος είναι πολύ δύσχρηστος και έτσι για τη μέτρηση μιας δύναμης διαλέγουμε την μέθοδο της μέτρησης της παραμόρφωσης (επιμήκυνσης) του ελατηρίου στο οποίο ασκείται.

Θα πούμε περισσότερα αφού πρώτα περιγράψω τη σχέση (νόμο) μεταξύ της επιμήκυνσης ενός ελατηρίου και της δύναμης που προκαλεί αυτή την επιμήκυνση. Εκτελούμε το ακόλουθο πείραμα: Σε ένα ελατήριο το οποίο είναι αναρτημένο κατακόρυφα σε ακλόνητο σημείο, κρεμάμε μια μάζα η οποία ασκεί δύναμη F στο ελατήριο. Μετράμε την επιμήκυνση του ελατηρίου η οποία είναι x. Στη συνέχεια κρεμάμε διπλάσια μάζα στο ελατήριο, που ασκεί διπλασια δύναμη 2F. (Στη Φυσική αποδεικνύεται ότι το βάρος ενός σώματος είναι ανάλογο με τη μάζα του). Βλέπουμε ότι το ελατήριο επιμηκύνεται κατά διπλάσια απόσταση 2x. Στη συνέχεια κρεμάμε τριπλάσια μάζα που ασκεί τριπλάσια δύναμη στο ελατήριο 3F. Βλέπουμε τώρα ότι, η επιμήκυνση του ελατηρίου τριπλασιάζεται σε 3x.

Γενικεύοντας καταλήγουμε στο συμπέρασμα το οποίο διατύπωσε το 17^ο αιώνα ο Άγγλος φυσικός Robert Hook:    Η επιμήκυνση x ενός ελατηρίου είναι ανάλογη της δύναμης F που ασκείται πάνω σ’ αυτό. Δηλαδή:

F = K∙x

Η σταθερά αναλογίας Κ είναι χαρακτηριστική σταθερά και έχει συγκεκριμένη τιμή για κάθε ελατήριο.

Έτσι για να μετρήσουμε μια δύναμη, μετράμε την επιμήκυνση που προκαλεί όταν ασκηθεί σε ελατήριο και μ’ αυτό τον τρόπο, κατασκευάζουμε όργανα μέτρησης δυνάμεων που λέγονται δυναμόμετρα.

Διανυσματικός χαρακτήρας της δύναμης

Ο ποδοσφαιριστής που εκτελεί πέναλτι, κτυπά με το πόδι του την ακίνητη μπάλα με συγκεκριμένο τρόπο, ώστε να κινηθεί με την κατεύθυνση της ταχύτητας που θέλει. Επειδή η ταχύτητα είναι διανυσματικό μέγεθος, που εκτός από μέτρο έχει και κατεύθυνση, καταλαβαίνουμε ότι και η δύναμη που προκαλεί τη μεταβολή της ταχύτητας θα είναι και αυτή διανυσματικό μέγεθος.

Η δύναμη ως διανυσματικό μέγεθος χαρακτηρίζεται από:
1] Το μέτρο που δείχνει πόσο μεγάλη είναι η δύναμή και εκφράζεται σε Newton.
2] Την κατεύθυνση (διεύθυνση και φορά) που δείχνει προς τα που ενεργεί η δύναμη.
3] Το σημείο εφαρμογής που δείχνει σε ποιο σημείο του σώματος ενεργεί η δύναμη.

Η δύναμη παριστάνεται με διάνυσμα, που δεν είναι τίποτε άλλο από ένα βέλος (ένα ευθύγραμμο τμήμα που το ένα άκρο του το έχουμε ονομάσει αρχή και το άλλο τέλος). Το μήκος του διανύσματος είναι ανάλογο του μέτρου της δύναμης, δηλαδή σχεδιάζουμε το διάνυσμα σε κατάλληλη κλίμακα. Έτσι αν εκλέξουμε αυθαίρετα 1cm να αντιστοιχεί σε 1Ν, τότε μια δύναμη μέτρου 6Ν παριστάνεται με ένα διάνυσμα μήκους 6cm.

Εκτελούμε τα παρακάτω πειράματα: Έχουμε ένα αυτοκινητάκι που κινείται με μπαταρίες και το αφήνουμε να κινείται ευθύγραμμα. Με ένα νήμα που το δένουμε στο πίσω μέρος, του ασκούμε δύναμη παράλληλη και αντίθετη με την κίνηση του, δηλαδή στην ταχύτητα του. Παρατηρούμε ότι το αυτοκινητάκι θα συνεχίσει να κινείται ευθύγραμμα αλλά με μειούμενη ταχύτητα μέχρι να σταματήσει. Συμπέρασμα: Μια δύναμη που ασκείται με την ίδια διεύθυνση με τη ταχύτητα του σώματος, προκαλεί μεταβολή στην ταχύτητα μόνο στο μέτρο της.

Στο ίδιο αυτοκινητάκι που κινείται, δένουμε ένα νήμα πάνω σε αυτό στο πλάι και το άλλο το δένουμε σταθερά κάπου στο πάτωμα. Παρατηρούμε ότι το αυτοκινητάκι κάνει κυκλική κίνηση τέτοια ώστε η δύναμη που του ασκείται από το νήμα είναι κάθετη στην ταχύτητα του. Συμπέρασμα: Μια δύναμη που ασκείται με τέτοιο τρόπο ώστε να είναι κάθετη στην ταχύτητα του σώματος , προκαλεί μεταβολή στην ταχύτητα μόνο στην κατεύθυνση της.

Δυο σημαντικές δυνάμεις στον κόσμο: Βάρος και Τριβή

Βαρυτική δύναμη.

Εκτελούμε το εξής πείραμα: Από κάποιο ύψος αφήνουμε να πέσει ένα κέρμα. Παρατηρούμε ότι θα πέσει στη Γη με διαρκώς αυξανόμενη ταχύτητα. Εκτελούμε και ένα άλλο πείραμα: ρίχνουμε ένα κέρμα προς τα πάνω. Παρατηρούμε ότι η ταχύτητα του κέρματος θα μειώνεται έως φτάσει το μέγιστο ύψος και από εκεί θα πέσει, με ταχύτητα διαρκώς αυξανόμενη. Και στις δυο αυτές περιπτώσεις κατά την κίνηση του κέρματος έχουμε μεταβολή της κινητικής κατάστασης του.

Σύμφωνα με τον Νεύτωνα, κάποιο αίτιο θα προκαλεί αυτή τη μεταβολή. Αυτό το αίτιο είναι η δύναμη βάρους που ασκεί η Γη στο κέρμα και γενικότερα σε κάθε σώμα. Την έννοια του βάρους τη συνέλαβε πρώτος ο Νεύτωνας, που όπως λέει η παράδοση όταν, είδε ένα μήλο να πέφτει κάτω από μια μηλιά, καθώς καθόταν κάτω από αυτή.

Η δύναμη του βάρους επεκτείνεται σε σώματα που βρίσκονται πέρα από την επιφάνεια της Γης, μέχρι και στα πιο απομακρυσμένα ουράνια σώματα. Έτσι ο Νεύτωνας διαπίστωσε ότι η Σελήνη περιστρέφεται σχεδόν κυκλικά γύρω από τη Γη, λόγω της βαρυτικής δύναμης που δέχεται από τη Γη. Γενικότερα οι πλανήτες στο ηλιακό μας σύστημα, περιστρέφονται γύρω από τον Ήλιο, λόγω της βαρυτικής δύναμης που δέχονται από αυτόν. Συνεπώς οι κινήσεις των σωμάτων στο σύμπαν καθορίζονται από τις ελκτικές βαρυτικές δυνάμεις.

Η Γη ασκεί βαρυτική δύναμη σε οποιοδήποτε σώμα ανεξάρτητα από την κατάσταση του (στερεά, υγρή, αέρια κατάσταση) και ανεξάρτητα από τον τρόπο που κινείται (ακίνητο στο έδαφος, πέφτει ή ανυψώνεται). Το βάρος είναι ελκτική δύναμη με διεύθυνση κατακόρυφη (η ευθεία που ορίζει η ακτίνα της της Γης σ’ αυτό τον τόπο) και φορά προς το κέντρο της Γης. Το βάρος που δέχεται ένα σώμα εξαρτάται από τη μάζα του. Τα σώματα  μεγάλης μάζας έχουν μεγαλύτερο βάρος από τα σώματα μικρότερης μάζας που βρίσκονται στον ίδιο τόπο. Επίσης το βάρος ενός σώματος εξαρτάται από την απόσταση του από το κέντρο της Γης. Έτσι καθώς ένα σώμα ανεβαίνει σε υψόμετρο, η βαρυτική δύναμη που δέχεται από τη Γη μειώνεται. Το βάρος ενός σώματος εξαρτάται και από τη μάζα του πλανήτη που το προκαλεί. Έτσι στην επιφάνεια της Σελήνης ένα σώμα έχει βάρος ίσο με το 1/6 του βάρους που το ίδιο σώμα έχει στην επιφάνεια της Γης. Πράγματι αυτό οφείλεται στο ότι η Σελήνη έχει μικρότερη μάζα από τη Γη και έτσι ασκεί μικρότερη ελκτική βαρυτική δύναμη.

Τριβή

Όταν σπρώχνουμε ένα κιβώτιο στο δάπεδο καταλαβαίνουμε ότι κάποια δύναμη το εμποδίζει να κινηθεί. Επίσης αν ωθήσουμε ένα σώμα να κινηθεί στο δάπεδο, θα παρατηρήσουμε ότι θα κινηθεί με μειούμενη ταχύτητα μέχρι να σταματήσει. Αλλά πιο το αίτιο (δύναμη) προκαλεί αυτή τη μεταβολή της κινητικής κατάστασης; Και στις δυο περιπτώσεις η δύναμη που ασκείται είναι η τριβή που αντιστέκεται στην κίνηση του σώματος. Δίνουμε τον ακόλουθο ορισμό:

Τριβή ονομάζεται η δύναμη που ασκείται από ένα σώμα σε ένα άλλο, όταν τα δύο σώματα βρίσκονται σε επαφή και το ένα κινείται ή τείνει να κινηθεί σε σχέση με το άλλο.

Η τριβή είναι δύναμη και έχει χαρακτηριστικά δύναμης σαν διανυσματικό μέγεθος και έχει κατεύθυνση (διεύθυνση και φορά) καθώς και μέτρο. Τα χαρακτηριστικά της δύναμης τριβής ορίζονται ως εξής:
1] Σημείο εφαρμογής: το σώμα πάνω στο οποίο ασκείται
2] Διεύθυνση παράλληλη στην επιφάνεια επαφής του σώματος.
3] Φορά είναι η αντίθετη στη φορά της κίνησης.
Η τριβή έχει στο Διεθνές Σύστημα Μονάδων, μονάδα μέτρησης το 1 Ν

Γνωρίζουμε ότι η δύναμη τριβής αντιτίθεται στην ολίσθηση του σώματος στο οποίο βρίσκεται σε επαφή με ένα άλλο. Καταλαβαίνουμε ότι η τριβή είναι χρήσιμη διότι μας βοηθά να περπατάμε χωρίς να γλιστράμε, όπως αντιθέτως συμβαίνει σε μια πίστα πάγου. Επίσης βοηθά στο αυτοκίνητο να κινείται και αυτό επειδή η τριβή επιτρέπει την κύλιση των τροχών στο έδαφος χωρίς να γλιστράνε, κι έτσι αυτό μπορεί να επιταχύνεται ή να επιβραδύνεται και να στρίβει αλλάζοντας την κατεύθυνση της ταχύτητας του.

Πως σχεδιάζουμε τις δυνάμεις

Γνωρίζουμε ότι το αίτιο της μεταβολής της κινητικής κατάστασης ενός σώματος είναι η δύναμη. Επομένως για να μπορέσουμε να βρούμε τον τρόπο κίνησης του σώματος αρκεί να βρούμε τις δυνάμεις που ασκούνται σε αυτό και να τις σχεδιάζουμε σωστά. Τα βήματα που ακολουθούμε για το σωστό σχεδιασμό των δυνάμεων είναι:

Πρώτο: Επιλέγουμε το σώμα που μας ενδιαφέρει. Υπενθυμίζουμε ότι θεωρούμε τα σώματα ως υλικά σημεία.

Δεύτερο: Σχεδιάζουμε τις δυνάμεις από απόσταση που ασκούνται στο σώμα. Σε ένα σώμα το οποίο βρίσκεται στην επιφάνεια της Γης ή σε κάποιο υψόμετρο ενεργεί το βάρος του. Σχεδιάζουμε το βάρος, με σημείο εφαρμογής το κέντρο βάρους του σώματος και διεύθυνση κατακόρυφη προς το κέντρο της Γης.

Τρίτο: Σχεδιάζουμε όλες τις δυνάμεις επαφής που ασκούνται στο σώμα.

Για τις δυνάμεις επαφής διακρίνουμε τις περιπτώσεις:

1] Ένα σώμα βρίσκεται σε επαφή πάνω σε ένα άλλο και στο οποίο ασκούνται δυο δυνάμεις όπως περιγράφονται παρακάτω: Α) Η κάθετη δύναμη που η επιφάνεια ασκεί στο σώμα και είναι κάθετη στην επιφάνεια επαφής και φορά από την επιφάνεια στο σώμα. Β) Η δύναμη τριβής που είναι η δύναμη στην οποία η επιφάνεια ασκεί στο σώμα αν αυτό ολισθαίνει ή τείνει να ολισθήσει πάνω στην επιφάνεια και είναι παράλληλη σ’ αυτή την επιφάνεια.

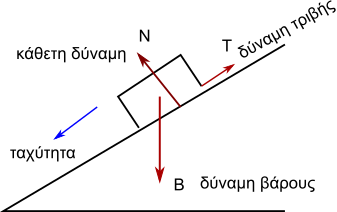
2] Ένα σώμα βρίσκεται σε επαφή με ένα τεντωμένο νήμα και το σώμα δέχεται δύναμη από το νήμα που ονομάζεται τάση του νήματος και έχει διεύθυνση του νήματος και φορά από το σώμα στο νήμα.

3] Ένα σώμα βρίσκεται σε επαφή με ένα ελατήριο, όπου στο σώμα ασκείται δύναμη από το ελατήριο με διεύθυνση ίδια με εκείνη του ελατηρίου. Αν το ελατήριο είναι τεντωμένο τότε η δύναμη ελατηρίου έχει φορά από το σώμα στο ελατήριο και αν είναι συμπιεσμένο η δύναμη ελατηρίου έχει φορά από το ελατήριο στο σώμα. Όταν το ελατήριο είναι στο φυσικό του μήκος δεν ασκεί δύναμη.

Σύνθεση και ανάλυση δυνάμεων

Συνισταμένη δυνάμεων

Σε προηγούμενη ενότητα είπαμε ότι ένα σώμα δέχεται επιδράσεις από τα σώματα του περιβάλλοντος του, που στη γλώσσα της φυσικής λέμε ότι στο σώμα ασκούνται δυνάμεις που προκαλούν τα σώματα του περιβάλλοντος του. Έτσι για να μπορέσουμε να βρούμε τον τρόπο κίνησης του σώματος στο οποίο ασκούνται δύο ή περισσότερες δυνάμεις, θα πρέπει να βρούμε την συνισταμένη τους. Δίνουμε τον ακόλουθο ορισμό:

Συνιστάμενη δύο ή περισσότερων δυνάμεων που ενεργούν σε ένα σώμα ονομάζεται η δύναμη που επιφέρει τα ίδια αποτελέσματα αν αντικαταστήσει τις δυνάμεις που ασκούνται στο σώμα.

Σύνθεση δυνάμεων ονομάζουμε την διαδικασία εύρεσης της συνισταμένης των δυνάμεων που δρουν σε ένα σώμα.

Σύνθεση δυνάμεων που έχουν την ίδια διεύθυνση

1] Σύνθεση δυο δυνάμεων F₁ και F₂ που έχουν ίδια κατεύθυνση (ίδια διεύθυνση και ίδια φορά)
Όταν σε ένα σώμα δρουν δυο δυνάμεις F₁ και F₂ της ίδιας διεύθυνσης (παράλληλες) και της ίδιας φοράς, η συνισταμένη τους έχει την ίδια διεύθυνση και φορά μ’ αυτές και μέτρο ίσο με το άθροισμα των δυο δυνάμεων.

2] Σύνθεση δυο δυνάμεων F₁ και F₂ που έχουν αντίθετες κατευθύνσεις (ίδια διεύθυνση και αντίθετες φορές)
Όταν σε ένα σώμα δρουν δυο δυνάμεις F₁ και F₂ της ίδιας διεύθυνσης (παράλληλες) αλλά έχουν αντίθετες φορές, η συνισταμένη τους έχει την ίδια διεύθυνση μ’ αυτές, αλλά φορά τη φορά της δύναμης με το μεγαλύτερο μέτρο και μέτρο ίσο με την διαφορά των μέτρων των δύο δυνάμεων. Δηλαδή:

F_ολ = F₁ – F₂   εάν ισχύει    F₁ > F₂
F_ολ = F₂ – F₁    εάν ισχύει    F₁ < F₂

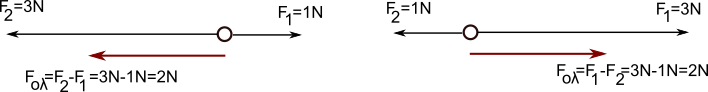
Αν οι δυο δυνάμεις έχουν την ίδια διεύθυνση, αντίθετες φορές αλλά ίσα μέτρα, η συνισταμένη τους είναι η μηδενική δύναμη και οι δυο αυτές δυνάμεις λέγονται αντίθετες.

Σύνθεση δυνάμεων με διαφορετικές διευθύνσεις

Σε προηγούμενη ενότητα υπολογίσαμε τη συνισταμένη δυο δυνάμεων που έχουν την ίδια διεύθυνση, με απλή πρόσθεση των μέτρων τους, αν έχουν την ίδια φορά και απλή αφαίρεση των μέτρων τους, αν έχουν αντίθετες φορές.

Στην περίπτωση που οι δυνάμεις έχουν διαφορετικές διευθύνσεις, όπως συχνά συμβαίνει στη φύση, η εύρεση της συνισταμένης πραγματοποιείται με τον κανόνα του παραλληλογράμμου. Για να υπολογίσουμε την συνισταμένη (σύνθεση δυνάμεων) των δυο δυνάμεων F₁ και F₂ που ασκούνται σε ένα σώμα, που έχουν διαφορετικές διευθύνσεις, ακολουθούμε την παρακάτω διαδικασία:

1] Σχεδιάζουμε τις δυνάμεις (διανύσματα) F₁ και F₂ με κοινή αρχή και υπό κλίμακα τέτοια ώστε το μήκος κάθε διανύσματος να είναι ανάλογο του μέτρου της δύναμης.
2] Από το τέλος της δύναμης F₁ φέρνουμε παράλληλη ευθεία στην F₂ και από το τέλος της δύναμης F₂ φέρνουμε παράλληλη στην F₁
3] Οι δυο αυτές παράλληλες ευθείες τέμνονται στο σημείο Α και σχηματίζουν παραλληλόγραμμο μαζί με τα διανύσματα των δυνάμεων.
4] Η διαγώνιος του παραλληλογράμμου με αρχή το σημείο Ο και τέλος το σημείο Α, δίνει τη συνισταμένη των δυνάμεων. Το μέτρο της βρίσκεται μετρώντας (στην ίδια κλίμακα) το μήκος της διαγώνιου ΟΑ και με ένα μοιρογνωμόνιο βρίσκουμε την κατεύθυνση της συνισταμένης, μετρώντας τη γωνία που σχηματίζει με τις δυνάμεις.

Στο παρακάτω σχήμα παίρνουμε μια ιδέα για τη σύνθεση δυο δυνάμεων με διαφορετικές διευθύνσεις. Παρατηρούμε ότι όσο μεγαλώνει η γωνία των δυο δυνάμεων, από 0 μοίρες έως 180 μοίρες, τόσο μειώνεται το μέτρο της συνισταμένης.

Αν οι διευθύνσεις των δυο δυνάμεων που θέλουμε να υπολογίσουμε την συνισταμένη τους είναι κάθετες μεταξύ τους, το μέτρο της συνισταμένης υπολογίζεται με το πυθαγόρειο θεώρημα. Δηλαδή:

F_ολ² = F₁² + F₂²

Δύναμη που ασκείται από τραχιά επιφάνεια

Όταν ένα σώμα βρίσκεται πάνω σε μια επιφάνεια, η οποία δεν είναι λεία και ολισθαίνει ή τείνει να ολισθήσει, τότε του ασκούνται δυο κάθετες μεταξύ τους δυνάμεις. Η κάθετη στην επιφάνεια επαφής, με φορά από το επίπεδο επαφής προς το σώμα και η δύναμη τριβής που είναι παράλληλη στην επιφάνεια επαφής. Για να βρούμε την συνισταμένη που ασκείται από την επιφάνεια στο σώμα κάνουμε σύνθεση των δυο αυτών δυνάμεων (F_N και Τ), απλά εφαρμόζοντας το Πυθαγόρειο Θεώρημα:

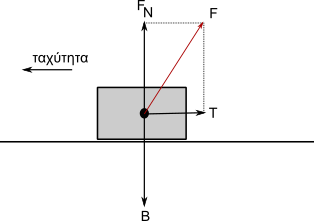
F² = F_N² + T²

Ανάλυση δύναμης

Η ανάλυση μιας δύναμης είναι η διαδικασία που κάνουμε για να βρούμε δυο δυνάμεις, που όταν αντικαταστήσουν την δύναμη, και ενεργηθούν στο ίδιο σώμα, προκαλούν το ίδιο αποτέλεσμα με την δύναμη που αντικαθιστούν.

Στις περισσότερες περιπτώσεις, η ανάλυση μιας δύναμης F γίνετε σε δυο δυνάμεις κάθετες μεταξύ τους και σε αυτή την περίπτωση η διαδικασία που ακολουθούμε είναι η ακόλουθη:

1] Σχεδιάζουμε την δύναμη καθώς και τους δυο κάθετους άξονες που θέλουμε να αναλύσουμε την δύναμη.
2] Από το τέλος της δύναμης F φέρνουμε παράλληλες ευθείες στους δυο άξονες.
3] Τα σημεία τομής των παράλληλων ευθειών με τους άξονες, ορίζουν τα άκρα των δυνάμεων που παριστάνουν τις συνιστώσες της δύναμης.
4] Μετράμε τα μήκη των δυο συνιστωσών δυνάμεων χρησιμοποιώντας την ίδια κλίμακα και υπολογίζουμε τα μέτρα των δύο δυνάμεων (συνιστώσες) που αναλύεται η δύναμη F.

Ανάλυση δύναμης σε κεκλιμένο επίπεδο

Οι κάθετοι άξονες που αναλύουμε μια δύναμη θα μπορούσαν να έχουν οποιαδήποτε διεύθυνση (αλλά κάθετοι μεταξύ τους), πέρα από οριζόντια και κατακόρυφη διεύθυνση. Συνήθως επιλέγουμε τον ένα άξονα στην διεύθυνση κίνησης του σώματος.

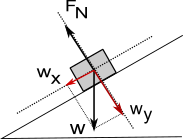
Στην περίπτωση της κίνησης ενός σώματος σε κεκλιμένο επίπεδο, επιλέγουμε τους άξονες τέτοιους ώστε ο ένας να είναι κάθετος στο κεκλιμένο επίπεδο και ο άλλος παράλληλος σ’ αυτό. Αναλύουμε το βάρος του σώματος σε μια συνιστώσα w_y στον άξονα κάθετο στο κεκλιμένο επίπεδο και μια συνιστώσα w_x στον άξονα παράλληλο στο κεκλιμένο επίπεδο. (βλέπε σχήμα).

Με την ανάλυση αυτή, μπορούμε να βρούμε εύκολα την κίνηση του σώματος στο κεκλιμένο επίπεδο, θεωρώντας λείες επιφάνειες και συνεπώς δεν έχουμε τριβές.