Ενέργεια: Μια θεμελιώδης έννοια της φυσικής
Η έννοια της ενέργειας εισήχθηκε για πρώτη φορά στη φυσική τον 17ο αιώνα από το Γαλιλαίο. Η ρίζα της λέξης ενέργεια είναι αρχαιοελληνική από τις λέξεις εν (μέσα) και έργο, δηλαδή σημαίνει την εσωτερική ικανότητα κάποιου να παράγει έργο. Αρχικά η έννοια ενέργεια δεν είχε συγκεκριμένο φυσικό περιεχόμενο. Μόλις πριν 200 χρόνια, οι επιστήμονες έδωσαν στην έννοια της ενέργειας αυστηρό επιστημονικό περιεχόμενο. Με την έννοια της ενέργειας, οι φυσικοί επιστήμονες κατάφεραν να περιγράψουν τα διάφορα φυσικά φαινόμενα με ενιαίο τρόπο. Έτσι την έννοια αυτή την συναντάμε σε φαινόμενα κίνησης των σωμάτων, σε ηλεκτρικά φαινόμενα, σε θερμικά φαινόμενα κ.α.
Στην έννοια της ενέργειας δεν μπορεί να αποδοθεί αυστηρός ορισμός. Είναι μια έννοια με την οποία είμαστε εξοικειωμένοι αλλά είναι δύσκολο να οριστεί με ακρίβεια, για το λόγο ότι είναι πρωταρχική έννοια. Όπως για παράδειγμα οι έννοιες του χώρου και του χρόνου είναι πρωταρχικές και δεν μπορούν να οριστούν πρωταρχικά. Μπορούμε να προσεγγίσουμε τη έννοια της ενέργειας λέγοντας ότι: «ενέργεια είναι ένα μέγεθος που εκφράζει την ικανότητα ενός φυσικού συστήματος να προκαλεί μεταβολές στο περιβάλλον του».
Η ενέργεια εμφανίζεται σε διάφορες μορφές, έτσι έχουμε τη μηχανική ενέργεια, την ηλεκτρική ενέργεια, τη θερμική ενέργεια, τη φωτεινή ενέργεια κ.α. Η ενέργεια μετατρέπεται από τη μια μορφή στην άλλη, μεταφέρεται από το ένα σώμα στο άλλο, αλλά η συνολική ενέργεια διατηρείται σταθερή.
Έργο και ενέργεια
Η έννοια του έργου χρησιμοποιείται στη γλώσσα της φυσικής και είναι «δανεισμένη» από την καθομιλουμένη αλλά χρησιμοποιείται με διαφορετικό τρόπο. Για να πάρουμε μια ιδέα της έννοιας του έργου στη φυσική, ας μελετήσουμε το εξής παράδειγμα:
θέλουμε να καρφώσουμε με ένα σφυρί ένα καρφί σε ένα κομμάτι ξύλο. Διαπιστώνουμε ότι το αποτέλεσμα σε κάθε χτύπημα του σφυριού εξαρτάται από το βάρος (δύναμη) του σφυριού και από τη διαδρομή (ύψος) που εκτελεί πριν χτυπήσει το καρφί. Το 1829 ο Γάλλος φυσικός Κοριόλις αποκάλεσε το γινόμενο της δύναμης με τη μετατόπιση ως έργο. Έτσι στο παράδειγμα μας, όσο μεγαλύτερο είναι το έργο του βάρους του σφυριού τόσο καλύτερα καρφώνει το καρφί.
Η ενέργεια μετατρέπεται από μια μορφή στην άλλη ή μεταφέρεται από το ένα σώμα στο άλλο με την εκτέλεση έργου δύναμης που κινεί το σημείο εφαρμογής της σε κάποια απόσταση.
Παράδειγμα: καθώς ανεβάζουμε τα βιβλία από το χαμηλότερο ράφι στο υψηλότερο σε μια βιβλιοθήκη τους ασκούμε δύναμη και με το έργο αυτής της δύναμης αποκτούν (δυναμική) ενέργεια, ενώ ταυτόχρονα κουραζόμαστε καταναλώνοντας από τον οργανισμό μας χημική ενέργεια. Χρησιμοποιούμε το φυσικό μέγεθος έργο για να εκφράσουμε την ποσότητα της ενέργειας που μεταφέρεται από εμάς στα βιβλία.
Έργο Δύναμης
Θεωρούμε ότι έχουμε ένα κιβώτιο και ασκώντας μια δύναμη το σηκώνουμε ψηλά. Η δύναμη αυτή παράγει έργο και κουραζόμαστε περισσότερο όσο μεγαλύτερη είναι η δύναμη και μεγαλύτερη είναι η διαδρομή. Επομένως το έργο εξαρτάται από τη δύναμη καθώς και από τη διαδρομή που ακολουθεί το σώμα.
Ορισμός Έργου
Όταν μια δύναμη F ασκείται σε ένα σώμα και είναι σταθερή και το σώμα μετακινείται ευθύγραμμα κατά την διεύθυνση της δύναμης το έργο w της δύναμης ορίζεται σαν το γινόμενο της δύναμης F επι τη μετατόπιση Δx. Δηλαδή:
W=F‧Δx
Μονάδες Έργου
Το έργο είναι παραγόμενο φυσικό μέγεθος άρα η μονάδα μέτρησης του προκύπτει από τον ορισμό του. Επομένως η μονάδα του έργου είναι η μονάδα της δύναμης 1 Newton επί τη μονάδα του μήκους 1m δηλαδή η μονάδα του έργου είναι 1 Ν.m. Αυτή η μονάδα ονομάζεται Joule ή συντετμημένα J προς τιμήν του Άγγλου Φυσικού Τζεϊμς Πρεσκοτ Τζάουλ. Δηλαδή:
1J = 1N‧m
Άρα έργο 1 joule παράγει δύναμη 1Ν που ασκείται στο σώμα το οποίο μετατοπίζεται κατά 1m κατά την κατεύθυνση της δύναμης.
Περιπτώσεις έργου: Το έργο είναι μονόμετρο μέγεθος άρα δεν έχει κατεύθυνση. Το έργο μπορεί να πάρει πραγματικές τιμές αρνητικές ή θετικές καθώς και το μηδέν.
1] Θετικό. Το έργο έχει θετική τιμή όταν η δύναμη και η μετατόπιση έχουν την ίδια κατεύθυνση. Θετικό έργο σημαίνει ότι προσφέρεται ενέργεια στο σώμα που ασκείται η δύναμη από αυτόν που ασκεί τη δύναμη.
2] Αρνητικό. Το έργο έχει αρνητική τιμή όταν η δύναμη και η μετατόπιση έχουν αντίθετη κατεύθυνση. Αρνητικό έργο σημαίνει αφαίρεση ενέργειας από το σώμα που ασκείται η δύναμη.
3] Μηδενικό. Μηδενικό έργο έχουμε όταν η δύναμη είναι κάθετη προς τη μετατόπιση του σώματος. Επίσης το έργο είναι μηδενικό όταν η δύναμη δεν μετατοπίζει το σημείο εφαρμογής της (το σώμα παραμένει ακίνητο).
Υπολογισμός έργου σταθερής δύναμης
Α] Δύναμη παράλληλη με τη μετατόπιση
Θέλουμε να υπολογίσουμε το έργο του βάρους w ενός σώματος το οποίο κινείται κατακόρυφα, πέφτει ή ανυψώνεται. Έστω ότι ένα σώμα βάρους w(=m‧g) πέφτει κατά ύψος h=Δx. Tο έργο του βάρους σε αυτή τη περίπτωση είναι θετικό διότι το βάρος και η μετατόπιση έχουν την ίδια κατεύθυνση. Επομένως το έργο του βάρους εδώ εκφράζεται:
Ww=w‧Δx ή Ww=w‧h ή Ww=m‧g‧h
Έστω ότι το σώμα βάρους w ανέρχεται (π.χ. το σηκώνουμε με το χέρι μας) κατά ύψος h. Επειδή η μετατόπιση (έχει φορά προς τα άνω) και η δύναμη του βάρους (έχει φορά προς τα κάτω) έχουν αντίθετες κατευθύνσεις το έργο του βάρους όταν ανεβαίνει το σώμα είναι αρνητικό.
Ww= –w‧h
Στην περίπτωση που ένας αρσιβαρίστας ασκεί δύναμη F στην μπάρα η οποία μετατοπίζεται ανυψωνόμενη προς τα πάνω, κατά h, το έργο αυτής της δύναμης είναι θετικό (δύναμη και μετατόπιση έχουν την ίδια κατεύθυνση) οπότε το έργο εκφράζεται
WF= F‧h
Β] Δύναμη πλάγια σε σχέση με τη μετατόπιση
Όταν έχουμε μια δύναμη μπορούμε να την αναλύσουμε ως προς δύο καθέτους άξονες, σε δύο κάθετες συνιστώσες, οι οποίες μαζί επιφέρουν το ίδιο αποτέλεσμα με την αρχική δύναμη.

Όταν σε ένα σώμα ασκείται σταθερή δύναμη της οποίας η κατεύθυνση σχηματίζει γωνία με τη μετατόπιση του σώματος, τότε αναλύουμε τη δύναμη σε μία συνιστώσα Fπ παράλληλη στη μετατόπιση και σε μια συνιστώσα FK κάθετη στη μετατόπιση. Tο έργο της πλάγιας δύναμης είναι ίσο με το άθροισμα των έργων των δυο συνιστωσών. Η κάθετη στη μετατόπιση συνιστώσα δεν παράγει έργο. Η παράλληλη στη μετατόπιση συνιστώσα παράγει έργο. Επομένως το έργο της δύναμης είναι ίσο:
W=Fπ‧Δx
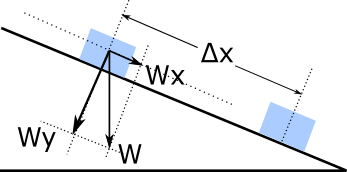
Mε ανάλογο τρόπο μπορούμε να βρούμε το έργο του βάρους ενός σώματος που γλιστράει σε κεκλιμένο επίπεδο. Αναλύουμε τη δύναμη του βάρους σε δύο κάθετες συνιστώσες, μια παράλληλη στο κεκλιμένο επίπεδο Wx και μια κάθετη στο κεκλιμένο επίπεδο Wy. Το ζητούμενο έργο του βάρους είναι ίσο με το έργο της παράλληλης συνιστώσας εφόσον η κάθετη συνιστώσα δεν παράγει έργο
W = Wx ‧Δx
Δυναμική – Κινητική ενέργεια
Δυναμική ενέργεια
Θεωρούμε την πολύ αργή ανύψωση ενός σώματος σε ένα ύψος. Για να τα καταφέρουμε πρέπει να ασκήσουμε μία κατακόρυφη δύναμη F με φορά προς τα πάνω που να έχει μέτρο ίσο με το βάρος για να έχουμε σχεδόν μηδενική ταχύτητα.
Το έργο της δύναμης F που ασκούμε στο σώμα υπολογίζεται ως εξής:
WF = F ‧ h = w ‧ h = m ‧ g ‧ h
Το έργο της δύναμης F υποδηλώνει την ενέργεια που δίνουμε στο σώμα για να βρεθεί σ΄ αυτό το ύψος h. Σύμφωνα με την αρχή διατήρησης της ενέργειας, η ενέργεια που δίνουμε στο σώμα μέσω του έργου της δύναμης F αποθηκεύεται στην ονομαζόμενη δυναμική ενέργεια λόγω βαρύτητας. Μπορούμε να πούμε ότι η ενέργεια αφαιρείται μέσω του έργου του βάρους και αποθηκεύεται σε δυναμική ενέργεια.
Κάθε φορά που κάνουμε χρήση της έννοιας της Δυναμικής ενέργειας πρέπει να ορίσουμε το επίπεδο μηδενικής δυναμικής ενέργειας. Με αυτό τον τρόπο σε κάθε θέση του σώματος σ΄αυτό το επίπεδο έχει εξ ορισμού μηδενική Δυναμική ενέργεια. Στο παράδειγμα μας θεωρούμε ως επίπεδο μηδενικής δυναμικής ενέργειας το επίπεδο του εδάφους.
Έχουμε τον εξής ορισμό: Δυναμική ενέργεια λόγω βαρύτητας ονομάζουμε το έργο της δύναμης που ανυψώνει αργά –αργά το σώμα από το επίπεδο μηδενικής δυναμικής ενέργειας στη θέση που βρίσκεται. Η δυναμική ενέργεια συμβολίζεται με το γράμμα U και δίνεται από τη σχέση:
U = m ‧ g ‧ h
όπου h το ύψος από τη θέση μηδενικής δυναμικής ενέργειας, m η μάζα του σώματος και g η επιτάχυνση της βαρύτητας.
Μονάδα δυναμικής ενέργειας στο Διεθνές Σύστημα μονάδων S.J είναι το Joule
1J = 1 N . m
Ένας άλλος ισοδύναμος ορισμός της δυναμικής ενέργειας είναι:
Δυναμική ενέργεια λόγω βαρύτητας ονομάζουμε το έργο του βάρους του σώματος κατά τη μεταφορά του από το σημείο που βρίσκεται προς το σημείο μηδενικής δυναμικής ενέργειας.
Αποδείξαμε σε προηγούμενη ενότητα ότι το έργο του βάρους από μια αρχική θέση σε μια τελική είναι ανεξάρτητο από τη διαδρομή (ίδιο για κάθε διαδρομή) και εξαρτάται από την αρχική και τελική θέση.
Έτσι μπορούμε να καταλάβουμε ότι η Δυναμική ενέργεια λόγω βαρύτητας έχει την ίδια τιμή σε μία θέση κάθε φορά που θα βρεθεί σ΄αυτή.
Ένα σώμα που πάει από τη θέση Α με δυναμική ενέργεια UA στη θέση Β με δυναμική ενέργεια UB το έργο του βάρους είναι το ίδιο για οποιαδήποτε διαδρομή από τη θέση Α στη θέση Β και ίσο με τη μεταβολή της δυναμικής ενέργειας UA – UB
Βαρυτική Δυναμική Ενέργεια
Επειδή ένα σώμα μπορεί να βρίσκεται είτε στο έδαφος είτε σε ένα ύψος πάνω από αυτό, θεωρούμε το επίπεδο Μηδενικής Δυναμικής Ενεργείας το οριζόντιο επίπεδο που ορίζεται από το έδαφος (ή το δάπεδο).

Σε ορισμένα προβλήματα μπορεί να είναι ευκολότερο να διαλέξουμε επίπεδο Μηδενικής Δυναμικής Ενέργειας αντί για το δάπεδο την επιφάνεια ενός οριζόντιου τραπεζιού ύψους h.Έστω η αρχική θέση Α και η τελική θέση Β έχουν ύψη ως προς το οριζόντιο τραπέζι h’A και h’B αντίστοιχα, θα είναι hA = h’A + h και hB = h’B + h. ( hA και hB είναι τα ύψη των θέσεων Α και Β από το οριζόντιο δάπεδο, αντίστοιχα)
H μεταβολή της δυναμικής ενέργειας από τη θέση Α στη θέση Β μπορεί να γραφτεί :
ΔU = mg (hB-hA) = mg [(h’B + h) – (h’A + h)] =
= mg (h’B + h – h’A – h) = mg (h’B – h’A) = ΔU
Συμπεραίνουμε ότι η μεταβολή της δυναμικής ενέργειας ενός σώματος λόγω της βαρύτητας είναι ανεξάρτητη από την εκλογή του επιπέδου Μηδενικής βαρύτητας και εξαρτάται μόνο από τις θέσεις αυτές και είναι σταθερή για κάθε διαδρομή από τη θέση Α στη θέση Β.
Δυναμική Ενέργεια και Δυνάμεις
Υπάρχουν άλλου τύπου δυνάμεις που κάνουν ένα σώμα να έχει δυναμική ενέργεια. Ένας πλανήτης που περιφέρεται γύρω από τον ήλιο, έχει εκτός από κινητική ενέργεια, βαρυτική δυναμική ενέργεια λόγω της βαρυτικής ελκτικής δύναμης που ασκεί ο ήλιος στον πλανήτη. Επίσης, ένα ηλεκτρόνιο που περιφέρεται γύρω από τον πυρήνα ενός ατόμου έχει ηλεκτρική δυναμική ενέργεια λόγω της ελκτικής ηλεκτρικής δύναμης που του ασκεί ο πυρήνας.
Αν ασκήσουμε μια δύναμη F και συμπιέσουμε ένα ελατήριο, η ενέργεια που δίνουμε μέσω του έργου της F, είναι W = F ‧ Δx, η οποία αποθηκεύεται ως δυναμική ενέργεια στο ελατήριο.
Γενικά όσα σώματα υφίσταται ελαστικές παραμορφώσεις, δηλαδή όταν τα παραμορφώνουμε και τα αφήνουμε ελεύθερα, αποκτούν το αρχικό τους σχήμα, αυτά τα σώματα αποκτούν δυναμική ενέργεια λόγω παραμόρφωσης. Η δυναμική ενέργεια λόγω ελαστικής παραμόρφωσης ισούται με το έργο της δύναμης που τους ασκήθηκε για να τα παραμορφώσει.
Η δυναμική ενέργεια λόγω ελαστικής παραμόρφωσης εξαρτάται από τη θέση ή την κατάσταση του παραμορφωμένου σώματος και δεν εξαρτάται από τη διαδρομή (τροχιά) που ακολούθησε το σώμα για να φτάσει σε αυτή τη θέση ή κατάσταση.
Κινητική Ενέργεια
Ένα σώμα βρίσκεται ακίνητο σε ένα οριζόντιο δάπεδο που δεν υπάρχει τριβή. Κάποια στιγμή ασκούμε στο σώμα μια οριζόντια δύναμη και το σώμα θα αρχίσει να κινείται και βλέπουμε ότι η ταχύτητα του ολοένα να αυξάνεται. Το σώμα θα προσλάβει ενέργεια μέσω του έργου της F. Η ενέργεια που θα πάρει το σώμα μετατρέπεται σε μία μορφή ενέργειας που λέγεται κινητική.
Κινητική ενέργεια ονομάζουμε την ενέργεια που έχει ένα σώμα λόγω της ταχύτητάς του.
Διαπιστώνουμε ότι η κινητική ενέργεια είναι ανάλογη της μάζας ενός σώματος και ανάλογη του τετραγώνου της ταχύτητας. Συγκεκριμένα αποδεικνύεται ότι ένα σώμα μάζας m που έχει ταχύτητα u η κινητική του ενέργεια είναι ίση με:
Εκ = ½ ‧ m‧ u2
Mονάδα κινητικής ενέργειας, όπως και κάθε άλλης μορφής ενέργειας είναι το joule.