Η έννοια της ταχύτητας
Στη καθημερινή ζωή, χρησιμοποιούμε τον όρο «ταχύτητα» για να δείξουμε πόσο αργά ή γρήγορα κινείται ένα αντικείμενο. Η ταχύτητα εκφράζεται με το χρονικό διάστημα που διανύει το κινητό μια συγκεκριμένη απόσταση. Έτσι ο δρομέας σε ένα αγώνα δρόμου 100μ που κάνει το μικρότερο χρόνο είναι ο ταχύτερος. Επίσης η ταχύτητα εκφράζεται με το διάστημα που διανύει το κινητό σε συγκεκριμένο χρονικό διάστημα. Έτσι σε ένα αγώνα ράλι, το αυτοκίνητο που θα διανύσει τη μεγαλύτερη απόσταση σε συγκεκριμένο χρονικό διάστημα είναι και το ταχύτερο.
Βλέπουμε σε κάθε περίπτωση ότι, η ταχύτητα συνδέεται με δυο μεγέθη: το μήκος διαδρομής και το χρόνο. Όσο μεγαλύτερο είναι το μήκος της διαδρομής που διατρέχει ένα σώμα σε ορισμένο χρόνο τόσο πιο γρήγορα κινείται και επομένως τόσο πιο μεγάλη είναι η ταχύτητα του. Επίσης όσο μικρότερο χρόνο το σώμα διανύει μια συγκεκριμένη απόσταση τόσο πιο μεγάλη είναι η ταχύτητα του.
Μέση ταχύτητα
Στη φυσική ορίζουμε το φυσικό μέγεθος της «ταχύτητας» με συγκεκριμένο μαθηματικό τρόπο, ώστε να μπορούμε να τη μετρούμε και να της αποδίδουμε τιμές. Στη φυσική για να εκφράσουμε πόσο γρήγορα κινείται ένα σώμα, αναγάγουμε το πόση απόσταση διανύει μέσα σε χρόνο ίσο με την μονάδα χρόνου. Αυτό εκφράζεται με τη μέση ταχύτητα που ορίζεται ως εξής:
Ως μέση ταχύτητα υμ ορίζεται το πηλίκο του μήκους s της διαδρομής που διανύει το κινητό σε χρονικό διάστημα Δt προς αυτό το χρονικό διάστημα. Δηλαδή:
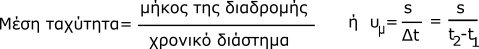
Όταν ως αρχή μέτρησης των χρόνων t1 έχει εκλεγεί το 0 (t1=0s) τότε το Δt ταυτίζεται με το t2 και συμβολίζουμε Δt=t και γράφουμε υμ=s/t
Η ταχύτητα είναι παράγωγο μέγεθος αφού ορίζεται βάσει των θεμελιωδών μεγεθών «μήκος» και «χρόνος». Μονάδα μέτρησης της ταχύτητας, στο Διεθνές Σύστημα μονάδων είναι το 1m/s. Πολλές φορές χρησιμοποιούμε και άλλες μονάδες, από τις οποίες η πιο πρακτική είναι το Km/h. Για να μετατρέψουμε το Km/h σε m/s εργαζόμαστε ως εξής:
1Km/h = 1000m/3600s = (1/3.6)m/s = 0.277m/s. Αντίστροφα 1m/s = 3.6Km/h
Η μέση ταχύτητα μας δίνει πληροφορίες, κατά μέσο όρο, πόσο γρήγορα διανύει ένα κινητό ένα διάστημα. Δεν μας δίνει πληροφορίες για το πόση γρήγορη ήταν η κίνηση σε κάθε θέση από την οποία πέρασε το κινητό. Για παράδειγμα, κατά τη διάρκεια ενός ταξιδιού, το αυτοκίνητο μπορεί να τρέξει με μεγαλύτερη ταχύτητα σε μια κατηφόρα, ενώ με μικρότερη σε μια ανηφόρα. Επίσης μπορεί να σταματήσει για λίγο σε ένα φανάρι. Η μέση ταχύτητα, μας δίνει «μια ιδέα» για το πόσο γρήγορα τρέχει. Π.χ. η ταχύτητα του αυτοκινήτου των 80Κm/h, δεν έχει καμία σχέση με την ταχύτητα του ήχου που είναι ίση με 1200Κm/h.
Η μέση ταχύτητα επειδή αναφέρεται στη συνολική διαδρομή, δεν δίνει πληροφορίες για τις μεταβολές της ταχύτητας σε κάθε θέση της διαδρομής, που εκφράζεται από την ένδειξη του ταχύμετρου του αυτοκινήτου και λέγεται στιγμιαία ταχύτητα. Η ταχύτητα που έχει ένα σώμα σε μια χρονική στιγμή λέγεται στιγμιαία ταχύτητα. Επειδή στις περισσότερες κινήσεις η στιγμιαία ταχύτητα δεν είναι σταθερή, δεν είναι ίση με τη μέση ταχύτητα. Αν η στιγμιαία ταχύτητα παραμένει σταθερή, τότε είναι ίση με τη μέση ταχύτητα.
Μέση διανυσματική ταχύτητα
Αν θέλουμε να περιγράψουμε την κίνηση ενός σώματος με μεγαλύτερη ακρίβεια, δεν αρκεί να γνωρίζουμε μόνο το μέτρο της ταχύτητας του με την οποία κινείται. Πράγματι, αν μας δίνεται η πληροφορία ότι ένα αυτοκίνητο περνά από τα διόδια του Σχηματαρίου με ταχύτητα 2Km/min (= 120Km/h), η πληροφορία αυτή δεν είναι αρκετή για να περιγράψουμε με ακρίβεια την κίνηση του αυτοκινήτου, διότι δεν γνωρίζουμε ότι στο επόμενο λεπτό θα κινηθεί κατά 2Κm προς την Αθήνα ή προς την Θεσσαλονίκη.
Στη Φυσική εκτός από το μέτρο της ταχύτητας μας ενδιαφέρει και η κατεύθυνση της κίνησης του σώματος. Έτσι ορίζεται ένα καινούργιο φυσικό μέγεθος η «μέση διανυσματική ταχύτητα» που ορίζεται ως αντί του μήκους διαδρομής χρησιμοποιήσουμε τη μετατόπιση.
Μέση διανυσματική ταχύτητα ορίζεται ως το πηλίκο της μετατόπισης του κινητού σε κάποιο χρονικό διάστημα προς αυτό το χρονικό διάστημα.

Η μέση διανυσματική ταχύτητα είναι διανυσματικό μέγεθος και παριστάνεται με την μαθηματική έννοια του διανύσματος που έχει κατεύθυνση ίδια με εκείνη της μετατοπίσεως.
Στις ευθύγραμμες κινήσεις η φορά της ταχύτητας παριστάνεται με το πρόσημο, έτσι για παράδειγμα, ένα σώμα που έχει μέση διανυσματική ταχύτητα υμ1=+30m/s κινείται προς τη θετική κατεύθυνση, ενώ όταν έχει μέση διανυσματική ταχύτητα υμ2=-30m/s κινείται προς την αρνητική κατεύθυνση.
Παράδειγμα. Παρατηρώντας τον άνδρα του σχήματος παίρνουμε τα εξής:

Ο άνδρας κινείται από τη θέση Α με xA=0 στη θέση Β με xB=+60m κατά την οποία η μετατόπιση του είναι:
ΔxAB = xB-xA = +60m-0 = +60m
Στη συνέχεια κινείται από τη θέση Β με xB=+60m στη θέση Γ με xΓ=-20m, κατά την οποία η μετατόπιση του είναι
ΔxBΓ = xΓ-xB = (-20m)-(60m) = -80m
Η ολική μετατόπιση του θα είναι:
ΔxΑΓ = ΔxAB+ΔxBΓ = (+60m)+(-80m) = -20m
Το μήκος της διαδρομής που διένυσε είναι
s = |ΔxAB| + |ΔxΒΓ| = |+60m|+|-80m| = 140m
Αν η κίνηση του άνδρα από τη θέση Α στη θέση Γ διήρκησε χρόνο t=20s, η μέση ταχύτητα του είναι
υμ = s/t = 140m/20s = 7m/s
ενώ η μέση διανυσματική ταχύτητα του από τη θέση Α στη θέση Γ είναι:
Στιγμιαία ταχύτητα
Αν πάρουμε τη μέση διανυσματική ταχύτητα για ένα πάρα πολύ μικρό χρονικό διάστημα γύρω από μια χρονική στιγμή t, τότε αυτή ορίζεται ως στιγμιαία διανυσματική ταχύτητα εκείνη τη χρονική στιγμή, που από τώρα και στο εξής, θα τη λέμε απλά στιγμιαία ταχύτητα.
Η στιγμιαία ταχύτητα είναι και αυτή διανυσματικό μέγεθος, που αποτελείται από το μέτρο και την κατεύθυνση ίδια με εκείνη της μετατόπισης. Για παράδειγμα, στην κίνηση του αεροπλάνου, ο πιλότος βλέπει στο ταχύμετρο το μέτρο της στιγμιαίας ταχύτητας του αεροπλάνου και στην πυξίδα την κατεύθυνση της στιγμιαίας ταχύτητας του.
Κίνηση με σταθερή ταχύτητα
Ευθύγραμμη ομαλή κίνηση
Θεωρούμε την κίνηση του ποδηλάτη όπως απεικονίζεται στο παρακάτω σχήμα, με τις τιμές των μεγεθών όπως παρουσιάζονται στο σχήμα.

Σε αυτή την κίνηση, υπολογίζοντας τη μέση ταχύτητα σε οποιοδήποτε χρονικό διάστημα Δt, βλέπουμε ότι έχει την ίδια τιμή και συγκεκριμένα τιμή ίση με 10m/s. Γενικότερα βρίσκουμε την ίδια τιμή για την μέση ταχύτητα, υπολογισμένη για κάθε μικρό ή μεγάλο χρονικό διάστημα, επομένως συμπεραίνουμε ότι το σώμα κινείται με σταθερή ταχύτητα. Συνεπώς:
Αν ένα σώμα κινείται ευθύγραμμα στην ίδια κατεύθυνση και η μέση ταχύτητα είναι η ίδια για οποιαδήποτε χρονικό διάστημα, τότε κινείται με σταθερή στιγμιαία ταχύτητα (σταθερό μέτρο και κατεύθυνση). Τώρα λέμε ότι το κινητό κάνει ευθύγραμμη ομαλή κίνηση. Ας δώσουμε το σχετικό ορισμό:
Ονομάζουμε ευθύγραμμη ομαλή κίνηση κάθε κίνηση στην οποία η στιγμιαία ταχύτητα διατηρείται σταθερή κατά μέτρο και κατεύθυνση. Δηλαδή:
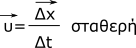
Αποδεικνύεται ότι όταν ένα σώμα κινείται με σταθερή στιγμιαία ταχύτητα (σταθερό μέτρο και κατεύθυνση) η κίνηση του είναι ευθύγραμμη της ίδιας κατεύθυνσης. Δηλαδή η κίνηση είναι ευθύγραμμη ομαλή.
Στην ευθύγραμμη ομαλή κίνηση, ισχύει:
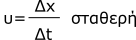
Από αυτή τη σχέση αποδεικνύεται ότι στην ευθύγραμμη ομαλή κίνηση, το κινητό σε ίσα χρονικά διαστήματα διανύει ίσες μετατοπίσεις.
Εξισώσεις της ευθύγραμμης ομαλής κίνησης
Οι εξισώσεις κίνησης είναι οι εξισώσεις οι οποίες περιγράφουν τον τρόπο που μεταβάλλονται με το χρόνο η θέση και η ταχύτητα του σώματος. Γνωρίζουμε την κίνηση ενός σώματος όταν γνωρίζουμε τις εξισώσεις κίνησης που δίνουν τη θέση και την ταχύτητα του σώματος σε οποιαδήποτε χρονική στιγμή.
Α. ΤΑΧΥΤΗΤΑ ΚΑΙ ΧΡΟΝΟΣ
Η εξίσωση ταχύτητας – χρόνου στην ευθύγραμμη ομαλή κίνηση
Στην ευθύγραμμη ομαλή κίνηση, η ταχύτητα δεν μεταβάλλεται, δηλαδή:
υ = σταθερή
Για να παραστήσουμε γραφικά αυτή την κίνηση, σχεδιάζουμε τη γραφική παράσταση της ταχύτητας σε συνάρτηση με το χρόνο.
Για να σχεδιάσουμε μια γραφική παράσταση, δημιουργούμε ένα πίνακα τιμών στον οποίο η πρώτη στήλη είναι οι χρονικές στιγμές και η δεύτερη στήλη είναι οι τιμές του μεγέθους του οποίου τη μεταβολή θέλουμε να μελετήσουμε.
Παρακάτω για μια ευθύγραμμη κίνηση, δίνεται ο πίνακας τιμών και σχεδιάζεται η γραφική παράσταση της ταχύτητας με το χρόνο:
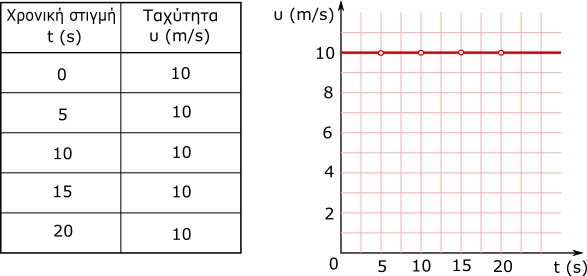
Παρατηρούμε ότι το διάγραμμα της ταχύτητας σε συνάρτηση με το χρόνο στην ευθύγραμμη ομαλή κίνηση είναι ευθεία παράλληλη με τον άξονα του χρόνου.
Β. ΜΕΤΑΤΟΠΙΣΗ, ΘΕΣΗ ΚΑΙ ΧΡΟΝΟΣ
Το πηλίκο της μετατόπισης δια το αντίστοιχο χρονικό διάστημα, είναι ίσο με την σταθερή ταχύτητα στην ευθύγραμμη ομαλή κίνηση.
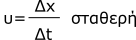
Λύνοντας αυτή τη σχέση ως προς τη μετατόπιση παίρνουμε
Δx = υ∙Δt
Παρατηρούμε ότι στην ευθύγραμμη ομαλή κίνηση, επειδή η ταχύτητα είναι σταθερή, η μετατόπιση Δx είναι ανάλογη με το χρονικό διάστημα που πραγματοποιείται. Δηλαδή σε διπλάσιο χρονικό διάστημα, το κινητό διανύει διπλάσια μετατόπιση, ενώ σε τριπλάσιο χρονικό διάστημα διανύει τριπλάσια μετατόπιση κ.τ.λ.
Η εξίσωση θέσης – χρόνου στην ευθύγραμμη ομαλή κίνηση
Θεωρούμε την ευθύγραμμη ομαλή κίνηση ενός αυτοκινήτου, με σταθερή ταχύτητα υ=20m/s που την χρονική στιγμή μηδέν t=0 βρίσκεται στο σημείο αναφοράς x=0.

Από τον ορισμό της ταχύτητας παίρνουμε για την μετατόπιση:
Δx = υ∙Δt
Αν το κινητό τη χρονική στιγμή t βρίσκεται στη θέση x, και για t=0 είναι x=0, εφαρμόζουμε στη σχέση αυτή:
Δt = tτελ – tαρχ = t -0 = t
Δx = xτελ – xαρχ = x – 0 = x
Συνεπώς η εξίσωση θέσης μπορεί να πάρει την μορφή:
x = υ∙t
Παρακάτω θα σχεδιάσουμε γραφικά τη σχέση της θέσης x με το χρόνο t, δηλαδή θα κάνουμε το διάγραμμα της θέσης σε συνάρτηση με το χρόνο στην ευθύγραμμη ομαλή κίνηση.
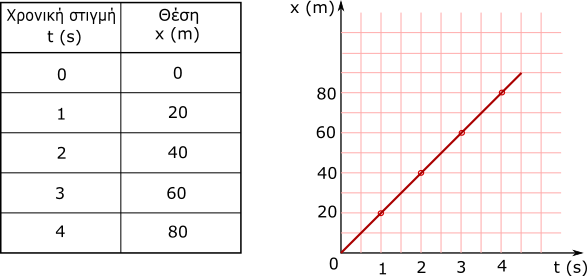
Κατασκευάζουμε τον πίνακα τιμών της σχέσης x = υ∙t (υ=20m/s σταθερή) που για διάφορες χρονικές τιμές υπολογίζουμε τη θέση του κινητού. Θέτουμε τα ζευγάρια των τιμών του πίνακα στη γραφική παράσταση και ενώνουμε τα σημεία. Παρατηρούμε ότι προκύπτει ευθεία. Άρα:
Το διάγραμμα θέσης σε συνάρτηση με το χρόνο σε μια ευθύγραμμη ομαλή κίνηση είναι ευθεία γραμμή.
Σώμα σε ηρεμία
Όταν ένα σώμα είναι ακίνητο σε σχέση με το σημείο αναφοράς, θεωρούμε ότι κάνει ομαλή κίνηση με ταχύτητα μηδέν.
Όταν ένα σώμα είναι ακίνητο, τότε το διάγραμμα της ταχύτητας με το χρόνο συμπίπτει με τον άξονα του χρόνου (ταχύτητα μηδέν).
Όταν ένα σώμα είναι ακίνητο σε μια θέση διαφορετική από το σημείο αναφοράς, το διάγραμμα θέσης σε συνάρτηση με το χρόνο είναι μια ευθεία παράλληλη στον άξονα του χρόνου. Αν είναι ακίνητο στη θέση αναφοράς (x=0) η ευθεία του διαγράμματος θέσης -χρόνου συμπίπτει με τον άξονα του χρόνου.
Κίνηση με μεταβαλλόμενη ταχύτητα
Ορισμός της μεταβαλλόμενης ταχύτητας
Η ταχύτητα στη Φυσική ορίζεται σαν διανυσματικό μέγεθος με χαρακτηριστικά το μέτρο, την διεύθυνση και τη φορά. Στην προηγούμενη ενότητα ορίσαμε τη σταθερή ταχύτητα όταν το διάνυσμα της ταχύτητας (μέτρο, διεύθυνση και φορά) είναι σταθερό. Αν το μέτρο ή/και η διεύθυνση ή/και η φορά της ταχύτητας μεταβάλλονται λέμε ότι η ταχύτητα μεταβάλλεται.
Παράδειγμα μεταβολής του μέτρου της ταχύτητας. Καθώς ένα αεροπλάνο κινείται ευθύγραμμα στο διάδρομο απογείωσης για να απογειωθεί, η ταχύτητα έχει σταθερή κατεύθυνση αλλά το μέτρο της αυξάνεται, ενώ όταν προσγειώνεται, η ταχύτητα έχει σταθερή κατεύθυνση αλλά το μέτρο της μειώνεται μέχρι να σταματήσει το αεροπλάνο. Εδώ έχουμε μεταβολή του μέτρου αλλά όχι της κατεύθυνσης (διεύθυνση και φορά) της ταχύτητας.
Στην καθημερινή ζωή λέμε ότι ένα όχημα επιταχύνεται όταν το μέτρο της ταχύτητας του αυξάνεται και επιβραδύνεται όταν το μέτρο της ταχύτητας του μειώνεται.
Παράδειγμα μεταβολής της κατεύθυνσης της ταχύτητας. Όταν ένα αυτοκίνητο μπαίνει σε μια στροφή και το ταχύμετρο δείχνει την ίδια ένδειξη, εδώ έχουμε την περίπτωση της κίνησης με το μέτρο της ταχύτητας να παραμένει σταθερό και να μεταβάλλεται η κατεύθυνση της. Εδώ λέμε ότι έχουμε κίνηση με μεταβαλλόμενη ταχύτητα.
Από τα παραπάνω παραδείγματα καταλαβαίνουμε ότι η ταχύτητα είναι διάνυσμα που έχει μέτρο και κατεύθυνση (διεύθυνση και φορά). Δίνουμε τον ακόλουθο ορισμό:
Κίνηση με μεταβαλλόμενη ταχύτητα λέγεται η κίνηση στην οποία, κατά την διάρκεια της, το διάνυσμα της στιγμιαίας ταχύτητας μεταβάλλεται ή κατά μέτρο ή κατά διεύθυνση ή και τα δύο.
Διαγράμματα και κινήσεις
Από τη μελέτη των διαγραμμάτων ταχύτητας – χρόνου και θέσης – χρόνου μπορούμε να καταλάβουμε το είδος της κίνησης που κάνει το κινητό.
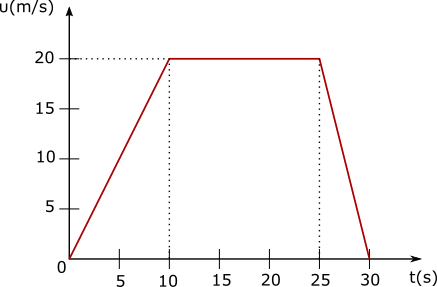
Διάγραμμα ταχύτητας – χρόνου.
Το διάγραμμα του παραπάνω σχήματος αντιστοιχεί σε ένα σύνθετο διάγραμμα ταχύτητας – χρόνου που αποτελείται από τα διαγράμματα των επιμέρους κινήσεων. Από το διάγραμμα βλέπουμε ότι το κινητό ξεκινά από τη χρονική στιγμή μηδέν με μηδενική ταχύτητα η οποία αυξάνεται έως τη χρονική στιγμή 10s και συνέχεια παραμένει σταθερή στην τιμή 20m/s μέχρι τη χρονική στιγμή 25s και ύστερα μειώνεται και μηδενίζεται τη χρονική στιγμή 30s. Το διάγραμμα αυτό θα μπορούσε να παραστήσει την κίνηση ενός δρομέα σε αγώνα δρόμου από την αφετηρία μέχρι να σταματήσει μετά τον τερματισμό.
Διάγραμμα θέσης–χρόνου
Αν ένα τμήμα σε ένα διάγραμμα θέσης – χρόνου μεταξύ δυο χρονικών στιγμών είναι ευθύγραμμο, τότε το κινητό κινείται με σταθερή ταχύτητα μεταξύ των δύο αυτών χρονικών στιγμών.
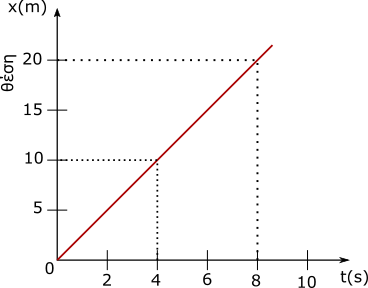
Το μέτρο της ταχύτητας είναι η κλίση του ευθύγραμμου τμήματος αυτού. Για να υπολογίσουμε την κλίση και συνεπώς την ταχύτητα, σημειώνουμε τη θέση x1 στην αρχή t1 του χρονικού διαστήματος και τη θέση x2 στο τέλος του χρονικού διαστήματος t2, οπότε η ταχύτητα (η κλίση) υπολογίζεται ως:
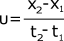
Παράδειγμα: Το διάγραμμα θέσης – χρόνου του παραπάνω σχήματος είναι ευθεία, άρα το κινητό κινείται με σταθερή ταχύτητα ίση με:
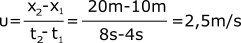
Το παρακάτω διάγραμμα θέσης – χρόνου του σχήματος παριστάνει μια σύνθετη κίνηση. Επειδή αποτελείται από ευθύγραμμα τμήματα η κίνηση στα αντίστοιχα χρονικά διαστήματα γίνεται με σταθερή ταχύτητα.
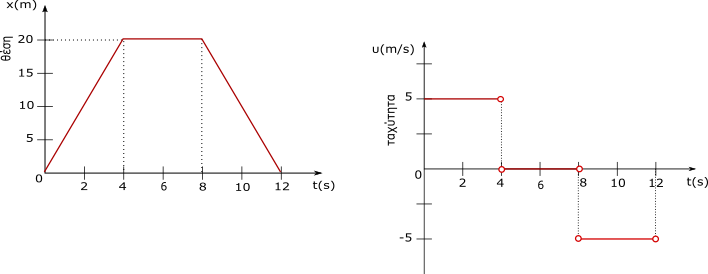
Το κινητό, που εδώ πρόκειται για μια μέλισσα, στο χρονικό διάστημα 0 – 4s κινείται με σταθερή ταχύτητα από την κηρήθρα προς το άνθος, στο χρονικό διάστημα 4s – 8s σταματά στο άνθος και στο χρονικό διάστημα 8s – 12s κινείται με σταθερή ταχύτητα προς την αντίθετη κατεύθυνση και επιστρέφει στο σημείο εκκίνησης. Το αντίστοιχο διάγραμμα ταχύτητας – χρόνου φαίνεται στο άλλο σχήμα.