Με τους νόμους του Νεύτωνα γίνεται κατανοητός ο τρόπος που οι δυνάμεις που ασκούνται σε ένα σώμα, καθορίζουν την κίνηση του. Αλλά ας πάρουμε τα πράγματα από την αρχή.
Ο πρώτος νόμος του Νεύτωνα
Έχουμε ένα κύβο πάνω σε ένα οριζόντιο δάπεδο και με το χέρι μας του δίνουμε μια ώθηση. Ο κύβος στην αρχή αποκτά κάποια ταχύτητα, κινείται λίγο πάνω στο δάπεδο και έπειτα σταματά. Από όσα είπαμε σε προηγούμενη ενότητα, εδώ έχουμε μεταβολή της κινητικής κατάστασης του κύβου, επομένως μια δύναμη (αίτιο) δρα πάνω του και το κάνει να σταματήσει. Αυτή είναι η δύναμη τριβής που ασκεί η επιφάνεια του δαπέδου στο κύβο με κατεύθυνση αντίθετη της κίνησης του.
Αν λειάνουμε τις επιφάνειες του δαπέδου και του κύβου που έρχονται σε επαφή και επαναλάβουμε το ίδιο πείραμα, παρατηρούμε ότι ο κύβος θα διανύσει μεγαλύτερη απόσταση και από αυτό καταλαβαίνουμε ότι η δύναμη τριβής θα είναι μικρότερη. Συμπερένουμε ότι, όσο πιο λείες είναι οι επιφάνειες που έρχονται σε επαφή, τόσο πιο μακρύτερα μετακινείται ο κύβος και τόσο πιο μικρή είναι η δύναμη τριβής.
Εκτελώντας ανάλογα πειράματα ο Γαλιλαίος οδηγήθηκε στο συμπέρασμα: Αν ήταν τέλεια λείο το οριζόντιο δάπεδο, τότε ένας κύβος τέλεια λείος με αρχική ταχύτητα, δεν θα σταματούσε ποτέ αλλά θα συνέχιζε να κινείται με την ίδια σταθερή ταχύτητα σε ευθεία γραμμή.
Επειδή στη φύση δεν υπάρχουν τέλεια λείες επιφάνειες, ένας θα αναρωτιούνταν αν έχει εφαρμογή αυτό το συμπέρασμα του Γαλιλαίου. Η απάντηση είναι ότι εφαρμόζεται όταν οι δυνάμεις γίνουν πολύ μικρές, όπως σε ένα αεροδιάδρομο οπότε η δύναμη τριβής εκεί είναι πολύ μικρή ή όταν έχουμε απότομες κινήσεις όπου η τριβή ασκείται σε πολύ μικρό χρονικό διάστημα και η επίδραση της τριβής μπορεί να θεωρηθεί αμελητέα.
Το 1687 ο Νεύτωνας δημοσίευσε ένα από τα σπουδαιότερα βιβλία της φυσικής, με τίτλο «Μαθηματικές αρχές της φυσικής φιλοσοφίας», στο οποίο διατυπώνονται οι τρείς θεμελιώδης νόμοι της Κλασσικής Μηχανικής. Ο πρώτος νόμος του Νεύτωνα που αποτελεί το πρώτο νόμο της κίνησης, που είναι η ολοκληρωμένη πρόταση του Γαλιλαίου και κάνοντας χρήση της έννοιας της δύναμης διατυπώνεται ως εξής:
Ένα σώμα παραμένει ακίνητο ή κινείται ευθύγραμμα με σταθερή ταχύτητα, αν δεν ασκείται πάνω του δύναμη ή αν ασκούνται δυνάμεις η συνισταμένη τους είναι μηδενική.
Διαφορετικά μπορούμε να πούμε ότι, αν σε ένα σώμα δεν επιδρά καμία δύναμη ή αν επιδρούν δυνάμεις με συνισταμένη μηδέν, τότε αν το σώμα ήταν αρχικά ακίνητο θα παραμείνει ακίνητο ή αν το σώμα κινείται θα συνεχίσει να κινείται με την ίδια σταθερή ταχύτητα. Σύμφωνα μ’ αυτόν τον πρώτο νόμο του Νεύτωνα, μπορούμε να συμπεράνουμε ότι, η δύναμη δεν είναι το αίτιο της κίνησης, αλλά το αίτιο της μεταβολής της κίνησης.
Η αδράνεια ως χαρακτηριστική ιδιότητα των σωμάτων
Ο πρώτος νόμος του Νεύτωνα συνδέεται με την χαρακτηριστική ιδιότητα των σωμάτων που είναι η αδράνεια, που με απλά λόγια είναι η ιδιότητα της αντίδρασης των σωμάτων στην επιτάχυνση τους και διατυπώνεται ως εξής:
Αδράνεια ονομάζουμε τη χαρακτηριστική ιδιότητα των υλικών σωμάτων να έχουν την τάση να διατηρούν την κινητική κατάσταση τους (ταχύτητα) και να αντιστέκονται σε κάθε μεταβολή της.
Ένα παράδειγμα που φαίνεται η αδράνεια των σωμάτων είναι του φρεναρίσματος ενός κινούμενου αυτοκινήτου. Όταν σε ένα κινούμενο αυτοκίνητο ο οδηγός πατήσει το φρένο, οι επιβάτες θα παταχθούν μπροστά, που είναι η εφαρμογή της ιδιότητας της αδράνειας που θέλει τα σώματα να διατηρούν την κινητική τους κατάσταση. Σε αυτό το παράδειγμα, το αυτοκίνητο μειώνει την ταχύτητα και οι επιβάτες πετάγονται μπροστά για να διατηρήσουν την κινητική κατάσταση τους.
Ισορροπία υλικού σημείου
Στην καθημερινή γλώσσα, λέμε ότι ένα σώμα ισορροπεί όταν είναι ακίνητο. Στην γλώσσα της φυσικής επεκτείνεται αυτός ο ορισμός στον κάτωθι:
Ένα σώμα ισορροπεί όταν είναι ακίνητο ή όταν κινείται ευθύγραμμα με σταθερή ταχύτητα.
Έτσι, διότι σύμφωνα με τον πρώτο νόμο του Νεύτωνα οι καταστάσεις της ακινησίας και της ευθύγραμμης ομαλής κίνησης είναι ισοδύναμες. Έτσι ο πρώτος Νόμος του Νεύτωνα περικλείει τη συνθήκη ισορροπίας ως εξής:
Για να ισορροπεί ένα σώμα πρέπει η συνισταμένη των δυνάμεων που ασκούνται πάνω του να είναι μηδέν.
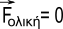
Παράδειγμα: Ένα βιβλίο που ισορροπεί πάνω σε ένα οριζόντιο τραπέζι, δρουν πάνω του δυο δυνάμεις: το βάρος του w που έχει διεύθυνση κατακόρυφη με φορά προς τα κάτω και η δύναμη επαφής FN που δέχεται το βιβλίο από το τραπέζι, η οποία είναι κάθετη στην επιφάνεια επαφής και επομένως έχει κατακόρυφη διεύθυνση με φορά προς τα πάνω. (Θεωρούμε ότι δεν ασκούνται δυνάμεις στατικής τριβής).
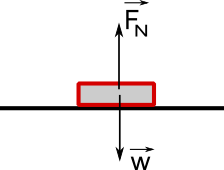
Αφού το βιβλίο ισορροπεί, τότε η συνισταμένη των δυο αυτών δυνάμεων είναι μηδενική. Επομένως:
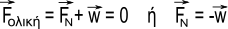
Αν πάρουμε την απόλυτη τιμή της τελευταίας σχέσης, βρίσκουμε για τα μέτρα των δυνάμεων:
FN=w
Ισορροπία στην περίπτωση που οι δυνάμεις δεν έχουν την ίδια διεύθυνση
Όταν σε ένα σώμα που ισορροπεί ασκούνται δυνάμεις που δεν έχουν την ίδια διεύθυνση, ισχύει η συνθήκη ισορροπίας η οποία μπορεί να γραφεί με διαφορετικό τρόπο:
Ορίζουμε δυο κάθετους άξονες και αναλύουμε όλες τις δυνάμεις σε συνιστώσες πάνω στους άξονες αυτούς. Γράφουμε τη συνθήκη ισορροπίας σε κάθε άξονα ως ΣFx=0 και ΣFy=0 όπου τα αθροίσματα αυτά είναι το αλγεβρικό άθροισμα των συνιστωσών των δυνάμεων σε κάθε ένα άξονα ξεχωριστά.
Δύναμη και μεταβολή της ταχύτητας
Δεύτερος νόμος του Νεύτωνα
Μια δύναμη που ασκείται πάνω σε ένα σώμα ορισμένης μάζας, έχει σαν αποτέλεσμα την μεταβολή της ταχύτητας του. Η σχέση μεταξύ της δύναμης , της μάζας του σώματος και της μεταβολής της ταχύτητας του, εκφράζεται από τον Δεύτερο Νόμο του Νεύτωνα. Για να κατανοήσουμε το νόμο ας πραγματοποιήσουμε τα παρακάτω πειράματα:
Πείραμα Α: Σε ένα οριζόντιο λείο επίπεδο (δεν υπάρχουν τριβές) σέρνουμε ένα κύβο ασκώντας του δύναμη F. Έπειτα σέρνουμε τον ίδιο κύβο ασκώντας διπλάσια δύναμη 2F. Τα αποτελέσματα των μετρήσεων φαίνονται στο σχήμα:
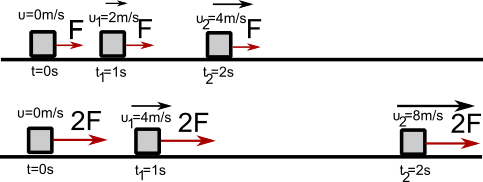
Παρατηρούμε ο κύβος όταν σέρνεται με δύναμη F, η ταχύτητα του μεταβάλλεται κατά 2m/s σε κάθε δευτερόλεπτο. Ο κύβος όταν σέρνεται με διπλάσια δύναμη 2F, η ταχύτητα του μεταβάλλεται κατά 4m/s κάθε δευτερόλεπτο.
Διαπιστώνουμε ότι όταν στον κύβο ενεργεί δύναμη διπλάσιου μέτρου, η μεταβολή της ταχύτητας του είναι διπλάσια στο ίδιο χρονικό διάστημα. Δηλαδή: Όσο μεγαλύτερη είναι η δύναμη που ασκείται σε ένα συγκεκριμένο σώμα, τόσο μεγαλύτερη μεταβολή της ταχύτητας έχουμε στο ίδιο χρονικό διάστημα.
Ορίζεται ένα φυσικό μέγεθος: ο ρυθμός μεταβολής της ταχύτητας, που εκφράζει πόσο γρήγορα μεταβάλλεται η ταχύτητα ενός σώματος. Αποδείξαμε πειραματικά ότι:
Ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι ανάλογος με το μέτρο της δύναμης που ενεργεί πάνω του.
Σε προηγούμενη ενότητα είπαμε ότι κάθε σώμα αντιστέκεται στη μεταβολή της κινητικής κατάστασης δηλαδή στη μεταβολή της ταχύτητας του. Για να το καταλάβουμε ας εκτελέσουμε το ακόλουθο πείραμα.
Πείραμα Β: Σε ένα λείο οριζόντιο επίπεδο σέρνουμε ένα κύβο με δύναμη F. Έπειτα διπλασιάζουμε τη μάζα του κύβου, βάζοντας όμοιο κύβο πάνω του και τους σέρνουμε με την ίδια δύναμη F. Τα αποτελέσματα των μετρήσεων φαίνονται στο σχήμα:
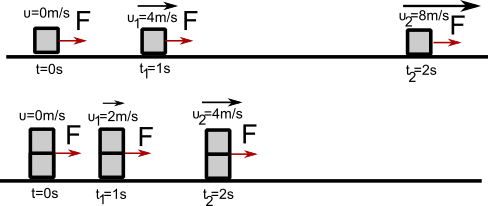
Παρατηρούμε ότι η ταχύτητα του διπλού κύβου, με τη διπλάσια μάζα, αυξάνεται με ρυθμό ο οποίος είναι ο μισός από το ρυθμό αύξησης της ταχύτητας που είχε ο μονός κύβος με μικρότερη μάζα. Δηλαδή:
Όσο μεγαλύτερη είναι η μάζα ενός σώματος, τόσο μικρότερη είναι η μεταβολή της ταχύτητας του στο ίδιο χρόνο που προκαλείται από την ίδια δύναμη. Ή με άλλα λόγια:
Όσο πιο μεγάλη είναι η μάζα τόσο δυσκολότερα μεταβάλλεται η ταχύτητα του. Επίσης γνωρίζουμε ότι η δυσκολία μεταβολής της κινητικής κατάστασης ενός σώματος εκφράζεται με την αδράνεια του. Επομένως μπορούμε να πούμε ότι:
Το μέτρο της αδράνειας ενός σώματος είναι η μάζα του.
Αποδείξαμε πειραματικά ότι: Ο ρυθμός μεταβολής της ταχύτητας ενός σώματος στο οποίο ενεργεί καθορισμένη δύναμη είναι αντιστρόφως ανάλογη με τη μάζα του σώματος.
Συνοψίζοντας όλα τα παραπάνω προκύπτει ο Δεύτερος Νόμος του Νεύτωνα, που συνοπτικά μπορεί να εκφραστεί με την πρόταση:
Δύναμη ίση (=) Μάζα επί (Χ) Ρυθμό μεταβολής της ταχύτητας.
Μάζα και Βάρος
Στην καθημερινή γλώσσα χρησιμοποιούμε τις έννοιες μάζα και βάρος χωρίς διάκριση. Ένας λόγος που γίνεται αυτό, είναι ότι για τον προσδιορισμό της μάζας, χρησιμοποιούμε τον ζυγό ισορροπίας, με τον οποίο συγκρίνουμε το βάρος ενός σώματος με το βάρος ενός προτύπου γνωστής μάζας. Επίσης και στα δύο αποδίδουμε την ίδια μονάδα. Π.χ. λέμε ότι το βάρος μου είναι 62 κιλά.
Στη γλώσσα της φυσικής το βάρος και η μάζα είναι εντελώς διαφορετικές έννοιες (φυσικά μεγέθη), που οι βασικές διαφορές τους είναι οι ακόλουθες:
1] Η μάζα είναι μονόμετρο μέγεθος, ενώ το βάρος είναι διανυσματικό μέγεθος.
2] Η μάζα εκφράζει το μέτρο της αδράνειας ενός σώματος, ενώ το βάρος είναι η βαρυτική δύναμη που δέχεται ένα σώμα από τη Γη.
3] Η μάζα ενός σώματος είναι η χαρακτηριστική τιμή του σώματος πάντα η ίδια σε όποιο σημείο στο σύμπαν και αν βρεθεί, ενώ το βάρος εξαρτάται από τον τόπο που βρίσκεται το σώμα.
4] Μονάδα μέτρησης της μάζας είναι το 1Kg, ενώ μονάδα μέτρησης του βάρους είναι το 1Ν.
Επιτάχυνση της βαρύτητας
Η βαρύτητα σε ένα τόπο χαρακτηρίζεται από ένα μέγεθος που λέγεται επιτάχυνση της βαρύτητας, που συμβολίζεται από το γράμμα g, και έχει χαρακτηριστική τιμή σε κάθε τόπο, καθώς και διαφέρει από τόπο σε τόπο. Έτσι η επιτάχυνση της βαρύτητας στην επιφάνεια της θάλασσας έχει τιμή 9.81m/s2 ενώ στην επιφάνεια της Σελήνης έχει τιμή 1,46m/s2
Η σχέση που συνδέει τη μάζα m και το βάρος w ενός σώματος σε ένα τόπο με επιτάχυνση της βαρύτητας g, είναι:
w = m ∙ g
Για παράδειγμα, για ένα σώμα με μάζα 1Κg έχει βάρος στην επιφάνεια της θάλασσας ίσο με:
WΓ = 1Kg ∙ 9,81m/s2 = 9,81N
Ενώ στην επιφάνεια της Σελήνης έχει βάρος
WΣ = 1Kg ∙ 1,46m/s2 = 1,46N
Δύναμη και αλληλεπίδραση
Τρίτος νόμος του Νεύτωνα
Πριν από 300 περίπου χρόνια, ο Νεύτωνας διακήρυξε ότι στη φύση υπάρχει συμμετρία και ότι όλες οι δυνάμεις πρέπει να θεωρούνται ως δυνάμεις αλληλεπίδρασης δυο σωμάτων, δηλαδή όταν ένα σώμα ασκεί σε κάποιο άλλο μια δύναμη τότε και το δεύτερο σώμα ασκεί στο πρώτο μια ίσου μέτρου αντίθετη δύναμη.
Πράγματι, ο ποδοσφαιριστής που εκτελεί πέναλτι, κλωτσά την μπάλα ασκώντας σ’ αυτή δύναμη, με αποτέλεσμα η μπάλα να κινηθεί. Αλλά και η μπάλα ασκεί μια αντίθετη δύναμη στο πόδι και γι΄αυτό νιώθει πόνο ο ποδοσφαιριστής. Όταν ο κωπηλάτης σέρνει τα κουπιά σε μια βάρκα, τότε με τα κουπιά ασκεί δύναμη στο νερό προς την αντίθετη που θέλει να κινήσει την βάρκα, ενώ το νερό ασκεί δύναμη στη βάρκα στην κατεύθυνση που θέλει να την κινήσει ο κωπηλάτης. Η Γη ασκεί βαρυτική δύναμη στη Σελήνη αλλά και η Σελήνη ασκεί βαρυτική δύναμη στη Γη.
Κάνοντας τέτοιες παρατηρήσεις ο Νεύτωνας, τις γενίκευσε και διατύπωσε το Τρίτο Νόμο της Μηχανικής, που είναι γνωστός σαν Τρίτος Νόμος του Νεύτωνα: Όταν ένα σώμα Α ασκεί μια δύναμη F σε ένα άλλο σώμα Β (δράση) τότε και το σώμα Β ασκεί δύναμη -F ίσου μέτρου και αντίθετης κατεύθυνσης στο σώμα Α (αντίδραση).
Σε κάθε δράση αντιστοιχεί μια αντίθετη αντίδραση και στη φύση ποτέ δεν εκδηλώνεται δράση χωρίς την αντίστοιχη αντίδραση. Η δράση και η αντίδραση ασκούνται μεταξύ δυο διαφορετικών σωμάτων. Επίσης δεν έχει νόημα να ρωτάμε ποια είναι η δράση και ποια η αντίδραση. Οι δυνάμεις δράση και αντίδραση εμφανίζονται ταυτόχρονα και συνυπάρχουν. Αυτό το ζευγάρι των δυνάμεων της δράσης και της αντίδρασης ασκούνται πάντοτε σε διαφορετικά σώματα και όχι στο ίδιο σώμα και γι’ αυτό δεν έχει νόημα η συνισταμένη τους.
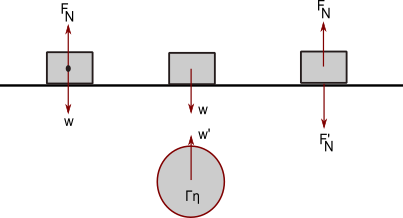
Παράδειγμα Α: Ένας κύβος ισορροπεί πάνω σε ένα οριζόντιο τραπέζι. Από τη συνθήκη ισορροπίας προκύπτει ότι η συνισταμένη δύναμη που ασκείται στο κύβο είναι μηδέν. Το βάρος του κύβου w εξισορροπείται από την κάθετη δύναμη FN που το τραπέζι ασκεί στο κύβο. Οι δυνάμεις αυτές έχουν ίσα μέτρα και αντίθετες κατευθύνσεις αλλά δεν αποτελούν ζεύγος δράσης-αντίδρασης. Αυτό επειδή προέρχονται από την αλληλεπίδραση του κύβου με δυο σώματα. Το βάρος είναι η δύναμη που ασκεί η Γη στον κύβο και η κάθετη δύναμη είναι η δύναμη που ασκεί το τραπέζι στον κύβο. Αν θεωρήσουμε το βάρος του κύβου w ως δράση τότε η αντίδραση της w’=-w είναι η βαρυτική δύναμη που ασκεί ο κύβος στη Γη και αν θεωρήσουμε την κάθετη δύναμη FN που ασκεί το τραπέζι στον κύβο ως δράση τότε η αντίδραση της είναι η δύναμη F’N =-FN ο κύβος ασκεί στο τραπέζι (βλέπε σχήμα)
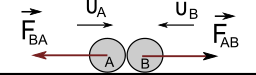
Παράδειγμα Β: Δυο σφαίρες συγκρούονται και η κατάσταση τους τη στιγμή της σύγκρουσης φαίνεται στο σχήμα. Τη στιγμή της κρούσης η σφαίρα Α ασκεί στη σφαίρα Β μια δύναμη FAB. Στο ίδιο χρονικό διάστημα και η σφαίρα Β ασκεί στη σφαίρα Α μια αντίθετη δύναμη FBA. Δηλαδή ![]() . Οι δυνάμεις αυτές έχουν σχέση δράσης – αντίδρασης.
. Οι δυνάμεις αυτές έχουν σχέση δράσης – αντίδρασης.
Εφαρμογές
Εφαρμογή Α: Από ένα ύψος αφήνουμε ελεύθερο ένα σώμα να πέσει στη Γη. Ένας θα έλεγε ότι το σώμα κινείται στη Γη και όχι η Γη προς το σώμα. Ερώτημα γιατί όχι και η Γη προς το σώμα αφού οι δυνάμεις που ασκούνται στο σώμα και στη Γη είναι ίσου μέτρου και αντίθετες;
Όπως περιγράφεται στον δεύτερο νόμο του Νεύτωνα, το αποτέλεσμα μιας δύναμης είναι η μεταβολή της ταχύτητας του σώματος με σταθερά αναλογίας τη μάζα του. Επειδή η Γη έχει πολύ μεγάλη μάζα (άρα και μεγάλη αδράνεια) η ταχύτητα της θα μεταβληθεί απειροελάχιστα ενώ το σώμα, επειδή έχει πολύ μικρή μάζα (πολύ μικρή αδράνεια), θα κινηθεί με μια αισθητή ταχύτητα προς τη Γη.
Εφαρμογή Β: Η ανύψωση ενός ελικοπτέρου εξηγείται ως εξής: Καθώς ο έλικας περιστρέφεται, τα μόρια του αέρα σπρώχνονται προς τα κάτω (δράση). Ταυτόχρονα τα μόρια του αέρα σπρώχνουν τον έλικα προς τα πάνω (αντίδραση). Έτσι μ’ αυτό τον τρόπο το ελικόπτερο ανυψώνεται. Παρόμοια είναι η εξήγηση για το πέταγμα των πουλιών και του αεροπλάνου.
Εφαρμογή Γ: Η κίνηση ενός πλοίου εξηγείται ως εξής: Καθώς η προπέλα περιστρέφεται, σπρώχνει το νερό προς τα πίσω (δράση). Ταυτόχρονα το νερό σπρώχνει την προπέλα προς τα εμπρός (αντίδραση). Έτσι μ’ αυτό τον τρόπο το πλοίο κινείται.