Νόμος του Κουλόμπ
Ο Γάλλος φυσικός Σαρλ Κουλόμπ (1736 – 1806) έπειτα από προσεκτικά πειράματα, ανακάλυψε τα χαρακτηριστικά της ηλεκτρικής δύναμης, από ποια μεγέθη και με πιο τρόπο εξαρτάται το μέτρο της ηλεκτρικής δύναμης από τα μεγέθη που υπεισέρχονται.
Ηλεκτρική δύναμη και απόσταση
Για να βρούμε πως σχετίζεται η ηλεκτρική δύναμη, με την οποία αλληλεπιδρούν δυο σημειακά φορτία q1 και q2 , που απέχουν μεταξύ τους απόσταση r, εκτελούμε το ακόλουθο πείραμα:

Παίρνουμε δυο μικρές θετικά φορτισμένες σφαίρες και τις τοποθετούμε σε απόσταση r. Μετράμε την ηλεκτρική δύναμη που ασκεί το ένα στο άλλο ηλεκτρικό φορτίο, έστω το μέτρο της είναι F. Έπειτα τοποθετούμε τις δύο ίδιες σφαίρες σε διπλάσια απόσταση 2r και μετράμε την ηλεκτρική δύναμη που ασκεί η μία φορτισμένη σφαίρα στην άλλη. Βλέπουμε ότι η ηλεκτρική δύναμη υποτετραπλασιάστηκε F/4 ή F/22. Τώρα τοποθετούμε τις ίδιες φορτισμένες σφαίρες σε τριπλάσια απόσταση και βλέπουμε ότι η μεταξύ τους ηλεκτρική δύναμη υποεννιαπλασιάστηκε F/9 ή F/32.
Συμπεραίνουμε ότι η ηλεκτρική δύναμη με την οποία αλληλεπιδρούν δυο φορτισμένες σφαίρες είναι αντιστρόφως ανάλογη του τετραγώνου της μεταξύ τους απόστασης.
Ηλεκτρική δύναμη και φορτίο
Για να βρούμε πως σχετίζεται η ηλεκτρική δύναμη με την οποία αλληλεπιδρούν δυο σημειακά φορτία q1 και q2 με την τιμή του ηλεκτρικού φορτίου τους, κάνουμε το ακόλουθο πείραμα:

Παίρνουμε δυο μικρές φορτισμένες σφαίρες με φορτία q1 και q2 και τις τοποθετούμε σε σταθερή απόσταση r μεταξύ τους. Μετράμε την ηλεκτρική δύναμη που ασκεί το ένα ηλεκτρικό φορτίο στο άλλο και έστω F το μέτρο της δύναμης. Παίρνουμε το ένα φορτίο και το διπλασιάζουμε 2q1 και μετράμε την μεταξύ τους ηλεκτρική δύναμη και βλέπουμε ότι διπλασιάστηκε 2F. Στη συνέχεια τετραπλασιάζουμε το αρχικό φορτίο 4q1 και μετρώντας την μεταξύ τους ηλεκτρική δύναμη βλέπουμε ότι τετραπλασιάστηκε 4F.
Συνεπώς η ηλεκτρική δύναμη αλληλεπίδρασης δυο μικρών φορτισμένων σφαιρών είναι ανάλογη του γινομένου των ηλεκτρικών φορτίων των σφαιρών κρατώντας την μεταξύ τους απόσταση σταθερή.
Πρέπει να σημειώσουμε ότι τα παραπάνω συμπεράσματα Κουλόμπ, ισχύουν για φορτισμένα σώματα των οποίων οι διαστάσεις τους είναι πολύ μικρές σε σχέση την μεταξύ τους απόσταση και γι’ αυτό ονομάζονται σημειακά φορτία. Επίσης ισχύουν και για ομοιογενής φορτισμένες σφαίρες.
Με τον συνδυασμό των παραπάνω συμπερασμάτων προκύπτει ο νόμος του Κουλόμπ, που τον διατύπωσε ο Γάλλος Σαρλ Κουλόμπ το 1789:
Το μέτρο της ηλεκτρικής δύναμης F με την οποία αλληλεπιδρούν δυο σημειακά φορτία q1 και q2 είναι ανάλογο του γινομένου των φορτίων και αντιστρόφως ανάλογο του τετραγώνου της μεταξύ τους απόστασης.
Μαθηματικά ο νόμος του Κουλόμπ εκφράζεται με τη σχέση:
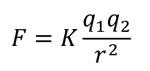
Το Κ είναι σταθερά αναλογίας και είναι ανεξάρτητη από τα ηλεκτρικά φορτία και την μεταξύ τους απόσταση. Η σταθερά Κ εξαρτάται από το υλικό στο οποίο μέσα βρίσκονται τα φορτισμένα σώματα και από το σύστημα μονάδων που χρησιμοποιούμε. Για το κενό και κατά προσέγγιση για τον αέρα η σταθερά Κ παίρνει τιμή:
Κ = 9·109Ν·m2/C2
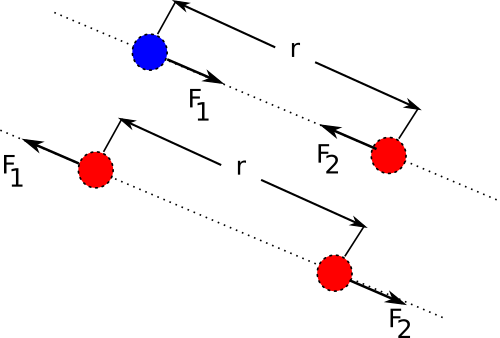
Οι δυνάμεις που ασκούνται μεταξύ δυο σημειακών φορτίων είναι διανύσματα, τα οποία έχουν διεύθυνση την ευθεία που περνά από δυο σημειακά φορτία και είναι απωστικές αν τα δυο ηλεκτρικά φορτία έχουν το ίδιο πρόσημο και ελκτικές αν τα δυο ηλεκτρικά φορτία έχουν διαφορετικό πρόσημο. Οι δυο δυνάμεις που ασκούνται μεταξύ δυο σημειακών ηλεκτρικών φορτίων, έχουν σχέση δράσης – αντίδρασης.
Οι ηλεκτρικές δυνάμεις έχουν κυρίαρχο ρόλο στο σχηματισμό των ατόμων και των μορίων, επομένως σε χημικές αντιδράσεις και βιολογικά φαινόμενα.
Αντίθετα, επειδή το ολικό ηλεκτρικό φορτίο των ουράνιων σωμάτων είναι ίσο με το μηδέν και για το λόγο ότι έχουν πολύ μεγάλη μάζα, αποδεικνύεται ότι οι κινήσεις των ουράνιων σωμάτων προσδιορίζονται μόνο από τις μεταξύ τους βαρυτικές δυνάμεις.
Έλξη μεταξύ φορτισμένου σώματος και ουδέτερου σώματος
Παρακάτω κάνοντας χρήση του νόμου του Κουλόμπ, θα εξηγήσουμε πως εμφανίζονται ελκτικές δυνάμεις μεταξύ ενός φορτισμένου σώματος και ενός ουδέτερου σώματος. Εκτελούμε το πείραμα:
Πλησιάζουμε μια θετικά φορτισμένη ράβδο στο αφόρτιστο μπαλάκι από αλουμινόχαρτο του ηλεκτρικού εκκρεμές. Το ουδέτερο μπαλάκι φορτίζεται με επαγωγή. Η περιοχή του μπαλακίου κοντά στη ράβδο φορτίζεται αρνητικά και έλκεται από την φορτισμένη ράβδο. Η περιοχή του μαλακίου που βρίσκεται μακριά από τη φορτισμένη ράβδο φορτίζεται θετικά και απωθείται από τη φορτισμένη ράβδο.
Σύμφωνα με το νόμο του Κουλόμπ οι ηλεκτρικές δυνάμεις σε ίδιες ποσότητες ηλεκτρικού φορτίου είναι αντιστρόφως ανάλογες του τετραγώνου της μεταξύ τους απόστασης. Έτσι η ελκτική ηλεκτρική δύναμη της φορτισμένης ράβδου στην αρνητικά φορτισμένη περιοχή του μπαλακίου είναι μεγαλύτερη από την απωστική ηλεκτρική δύναμη της φορτισμένης ράβδου στη θετικά φορτισμένη περιοχή του μπαλακίου. Έτσι ασκείται συνισταμένη δύναμη στο μπαλάκι η οποία είναι έλξη του μπαλακίου, από την φορτισμένη ράβδο.
Το ηλεκτρικό πεδίο
Στις προηγούμενες ενότητες είδαμε ότι τα φορτισμένα σώματα αλληλεπιδρούν ασκώντας ηλεκτρικές δυνάμεις μεταξύ τους, χωρίς να παρεμβάλλεται κάποιο υλικό, δηλαδή οι ηλεκτρικές δυνάμεις είναι δυνάμεις από απόσταση, όπως είναι οι μαγνητικές και οι βαρυτικές δυνάμεις. Ο Άγγλος φυσικός Μάικλ Φάραντεϊ για να περιγράψει τις ηλεκτρικές αλληλεπιδράσεις των σωμάτων από απόσταση, επινόησε την έννοια του ηλεκτρικού πεδίου.
Ηλεκτρική δύναμη και πεδίο
Εκτελούμε το ακόλουθο πείραμα: Παίρνουμε μια μεγάλη μεταλλική σφαίρα και την φορτίζουμε μέσω της ηλεκτροστατικής μηχανής Van der Graaft. Πλησιάζουμε ένα ηλεκτρικό εκκρεμές στη σφαίρα, το οποίο φορτίζεται με επαγωγή. Παρατηρούμε ότι σε όποιο σημείο κι αν τοποθετήσουμε το ηλεκτρικό εκκρεμές εκτρέπεται από την αρχική του θέση, δηλαδή πάνω στο μπαλάκι του εκκρεμούς ασκείται ηλεκτρική δύναμη από την φορτισμένη σφαίρα, κι αυτό σε κάθε σημείο γύρω από την φορτισμένη σφαίρα.
Συμπεραίνουμε ότι ο χώρος γύρω από τη σφαίρα απέκτησε την ιδιότητα, να ασκεί δυνάμεις σε ηλεκτρικά φορτία που τοποθετούνται σε κάθε σημείο του. Μπορούμε να πούμε ότι στο χώρο αυτό υπάρχει ηλεκτρικό πεδίο.
Ορισμός: Ηλεκτρικό πεδίο ονομάζεται μια περιοχή του χώρου, που απέκτησε την ιδιότητα ότι σε οποιοδήποτε σημείο της περιοχής κι αν τοποθετήσουμε ένα φορτισμένο σώμα, ασκούνται πάνω του ηλεκτρικές δυνάμεις.
Η ηλεκτρική δύναμη αλληλεπίδρασης μεταξύ δυο φορτισμένων σωμάτων, περιγράφεται με την έννοια του ηλεκτρικού πεδίου σε δυο βήματα:
α. Γύρω από κάθε φορτισμένο σώμα δημιουργείται ηλεκτρικό πεδίο
β. Τα φορτισμένα σώματα αλληλεπιδρούν μέσω των ηλεκτρικών πεδίων που δημιουργούν.
Για παράδειγμα, ας πάρουμε το άτομο όπως το περιγράψαμε σε προηγούμενη ενότητα. Ο πυρήνας του ατόμου δημιουργεί γύρω του ηλεκτρικό πεδίο, που ασκεί ηλεκτρική δύναμη στα ηλεκτρόνια του ατόμου. Αλλά και τα ηλεκτρόνια δημιουργούν ηλεκτρικό πεδίο, που ασκεί ηλεκτρική δύναμη στον πυρήνα.
Για να διαπιστώσουμε αν σε μια περιοχή του χώρου υπάρχει ηλεκτρικό πεδίο, φέρνουμε εκεί το φορτισμένο μπαλάκι του ηλεκτρικού εκκρεμούς. Αν εκτραπεί το ηλεκτρικό εκκρεμές από την αρχική του θέση, σημαίνει ότι υπάρχει ηλεκτρικό πεδίο εκεί.
Περιγραφή του ηλεκτρικού πεδίου
Επειδή το ηλεκτρικό πεδίο είναι μια ιδιότητα του χώρου, θα πρέπει να υπάρχει τρόπος να το περιγράψουμε. Ένας πρώτος τρόπος είναι με την ηλεκτρική δύναμη που ασκείται σε ένα φορτισμένο σώμα, στο σημείο του χώρου που θέλουμε να περιγράψουμε. Το μειονέκτημα αυτού του τρόπου είναι ότι η δύναμη αυτή εξαρτάται εκτός από το σημείο που βρίσκεται αλλά και από το μέγεθος του δοκιμαστικού ηλεκτρικού φορτίου. Όσο μεγαλύτερο είναι το δοκιμαστικό φορτίο που φέρνουμε τόσο μεγαλύτερη είναι η δύναμη που ασκεί σ’ αυτό το ηλεκτρικό πεδίο.
Μπορούμε να περιγράψουμε ένα ηλεκτρικό πεδίο σε ένα σημείο του χώρου αν φέρουμε δοκιμαστικό θετικό ηλεκτρικό φορτίο ενός Κουλόμπ. Με τον τρόπο αυτό περιγράφουμε το ηλεκτρικό πεδίο, χρησιμοποιώντας το μέγεθος που λέγεται ένταση του ηλεκτρικού φορτίου.
Ορισμός: Ένταση του ηλεκτρικού πεδίου σε ένα σημείο του, ορίζεται από την ηλεκτρική δύναμη που ασκείται από το πεδίο σε θετικό ηλεκτρικό φορτίο σε αυτό το σημείο, με μέγεθος ενός Κουλόμπ.
Ηλεκτρικές δυναμικές γραμμές
Το ηλεκτρικό πεδίο δεν μπορούμε να το αντιληφθούμε με τις αισθήσεις μας. Ο φυσικός Μάικλ Φάραντεϊ, για να περιγράψει και να δώσει μια οπτική εικόνα του ηλεκτρικού πεδίου, εισήγαγε τις ηλεκτρικές δυναμικές γραμμές που χρησιμοποιούμε ως και σήμερα.
Για να πάρουμε μια εικόνα των ηλεκτρικών δυναμικών γραμμών, θεωρούμε λεπτές μεταξωτές κλωστές μέσα στο ηλεκτρικό πεδίο. Οι κλωστές αυτές διατάσσονται σε γραμμές, ώστε να δείχνουν σε κάθε σημείο τους την διεύθυνση της δύναμης, που ασκείται σε ένα δοκιμαστικό θετικό φορτίο. Όπου συγκεντρώνονται περισσότερες κλωστές, η ηλεκτρική δύναμη είναι ισχυρότερη και οι δυναμικές γραμμές πυκνότερες.
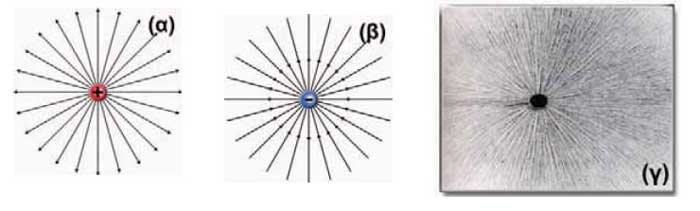
Οι ηλεκτρικές δυναμικές γραμμές, δίνουν πληροφορίες για την διεύθυνση και το μέτρο της ηλεκτρικής δύναμης (πάνω σε θετικό φορτίο ενός Κουλόμπ). Έτσι, η διεύθυνση των ηλεκτρικών δυναμικών γραμμών σε κάθε σημείο του πεδίου, συμπίπτει με την διεύθυνση της ηλεκτρικής δύναμης (και της έντασης του ηλεκτρικού πεδίου) σε αυτό το σημείο.
Η πυκνότητα των ηλεκτρικών δυναμικών γραμμών, δείχνει το πόσο ισχυρή είναι η ηλεκτρική δύναμη σε αυτό το σημείο. Όσο πιο πυκνές είναι οι ηλεκτρικές δυναμικές γραμμές, τόσο μεγαλύτερη είναι η ηλεκτρική δύναμη και συνεπώς η ένταση σε αυτό το σημείο.
Ένα σύστημα δυο παράλληλων μεταλλικών πλακών, οι οποίες είναι αντίθετα φορτισμένες, λέγεται πυκνωτής. Στο σχήμα φαίνεται δια μέσου των δυναμικών γραμμών, η παράσταση της έντασης του ηλεκτρικού πεδίου στο χώρο του πυκνωτή. Βλέπουμε ότι οι δυναμικές γραμμές, στο εσωτερικό του πυκνωτή είναι ευθείες παράλληλες και ισαπέχουσες και συνεπώς η πυκνότητα τους στο εσωτερικό του πυκνωτή είναι παντού σταθερή. Επομένως, το ηλεκτρικό πεδίο σε οποιαδήποτε σημείο στο εσωτερικό του πυκνωτή, ασκεί την ίδια ηλεκτρική δύναμη σε ένα δοκιμαστικό ηλεκτρικό φορτίο. Ένα τέτοιο ηλεκτρικό πεδίο έχει σταθερή ένταση και λέγεται ομογενές.
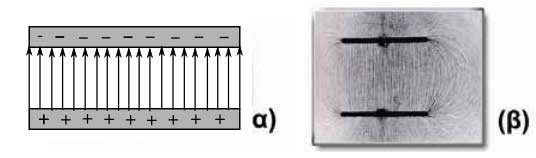
Ορισμός: Ομογενές ηλεκτρικό πεδίο, είναι εκείνο το πεδίο που οι ηλεκτρικές δυναμικές γραμμές του, είναι παράλληλες ευθείες και ισαπέχουσες, με αποτέλεσμα να ασκεί την ίδια δύναμη σε ένα ηλεκτρικό φορτίο σε όποιο σημείο του κι αν το τοποθετήσουμε. Η ένταση ενός ομογενούς πεδίου είναι σταθερή σε όλα τα σημεία του.
Ηλεκτρική θωράκιση
Στο σχήμα βλέπουμε τις δυναμικές γραμμές, που δημιουργούνται από μια φορτισμένη πλάκα και ένα αντίθετα φορτισμένο μεταλλικό κύλινδρο.

Παρατηρούμε ότι στο εσωτερικό του κυλίνδρου δεν υπάρχει ηλεκτρικό πεδίο (η ένταση ηλεκτρικού πεδίου στο εσωτερικό του κυλίνδρου είναι μηδέν). Αυτό που συμβαίνει είναι το εξής: Τα ηλεκτρόνια, πάνω στο μεταλλικό κύλινδρο, κατανέμονται με επαγωγή με τέτοιο τρόπο, ώστε το ηλεκτρικό πεδίο που δημιουργούν στο εσωτερικό του κυλίνδρου να είναι αντίθετο από το ηλεκτρικό πεδίο που δημιουργεί η φορτισμένη πλάκα. Το αποτέλεσμα είναι ότι, το ηλεκτρικό πεδίο μέσα στον κύλινδρο να είναι μηδέν και να μην υπάρχουν ηλεκτρικές δυναμικές γραμμές εκεί.
Ηλεκτρικό πεδίο και ενέργεια
Έχουμε μια ηλεκτροστατική μηχανή Wimshurst και τη θέτουμε σε λειτουργία. Αυτή έχει δυο σφαίρες που φορτίζονται αντίθετα κατά την λειτουργία της, η μια με θετικό φορτίο και η άλλη με αρνητικό φορτίο. Πλησιάζουμε στη θετικά φορτισμένη σφαίρα της μηχανής, το θετικά φορτισμένο μπαλάκι του ηλεκτρικού εκκρεμούς. Παρατηρούμε ότι το μπαλάκι κινείται από τη θετικά φορτισμένη σφαίρα της μηχανής προς την αρνητικά φορτισμένη σφαίρα.
Παρακάτω θα προσπαθήσουμε να ερμηνεύσουμε το φαινόμενο χρησιμοποιώντας τις έννοιες της ενέργειας και του ηλεκτρικού πεδίου. Το φορτισμένο μπαλάκι βρίσκεται μέσα στο ηλεκτρικό πεδίο, που δημιουργούν οι δυο αντίθετα φορτισμένες σφαίρες της μηχανής. Στο μπαλάκι ασκείται ηλεκτρική δύναμη και κινείται αποκτώντας κινητική ενέργεια.
Γνωρίζουμε ότι ενέργεια δεν παράγεται από το μηδέν, αλλά μετατρέπεται από τη μια μορφή στην άλλη. Έτσι, προκύπτει το ερώτημα: από ποια μορφή ενέργειας προέκυψε η κινητική ενέργεια του μπαλακίου; Για να απαντήσουμε σκεφτόμαστε ως εξής;
Το ηλεκτρικό πεδίο ασκεί ηλεκτρική δύναμη στο φορτισμένο μπαλάκι, σε όποιο σημείο κι αν βρεθεί. Έτσι το φορτισμένο μπαλάκι έχει ηλεκτρική δυναμική ενέργεια και έχει συγκεκριμένη τιμή σε όποιο σημείο μέσα στο ηλεκτρικό πεδίο κι αν βρεθεί. Έτσι η κινητική ενέργεια που αποκτά το φορτισμένο μπαλάκι, κατά την κίνηση του από μια αρχική θέση σε μια τελική θέση, είναι η διαφορά (η μεταβολή) της δυναμικής ενέργειας του φορτισμένου μπαλακίου στις θέσεις αυτές. Μάλιστα αυτή η μεταβολή της δυναμικής ενέργειας, είναι ίση με το έργο της ηλεκτρικής δύναμης του ηλεκτρικού πεδίου κατά την κίνηση του.
Παίρνουμε μια θετικά φορτισμένη σφαίρα και φέρνουμε κοντά σε αυτήν, στο σημείο Α, ένα θετικό δοκιμαστικό φορτίο. Επειδή στο δοκιμαστικό φορτίο ασκείται απωστική δύναμη, πρέπει να ασκήσουμε αντίθετη δύναμη F για να καταφέρουμε να το πλησιάσουμε. Συνεπώς ξοδεύουμε ενέργεια, για να φέρουμε το δοκιμαστικό φορτίο στη θέση Α, ίση με τη ηλεκτρική δυναμική ενέργεια που αποθηκεύεται στο δοκιμαστικό φορτίο στη θέση Α. Μάλιστα το έργο της δύναμης F είναι παραγόμενο και εκφράζει την ενέργεια που ξοδεύουμε με αποτέλεσμα να αποθηκευτεί σε ηλεκτρική δυναμική ενέργεια του δοκιμαστικού θετικού φορτίου στη θέση Α.
Για να φορτίσουμε ένα σώμα, του μεταφέρουμε σταδιακά το ηλεκτρικό φορτίο. Επειδή το φορτιζόμενο σώμα δημιουργεί γύρω του ηλεκτρικό πεδίο, για να του προσθέσουμε ηλεκτρικό φορτίο, πρέπει να ασκήσουμε δύναμη στο φορτίο για να μπορέσουμε να το πλησιάσουμε στο φορτιζόμενο σώμα. Η ενέργεια που προσφέρουμε στο ηλεκτρικό φορτίο που προσθέτουμε, αποθηκεύεται ως δυναμική ενέργεια στο ηλεκτρικό φορτίο του σώματος που φορτίζουμε.