Ορισμός περιοδικών κινήσεων
Μια κίνηση που επαναλαμβάνεται σε ίσα χρονικά διαστήματα, ονομάζεται περιοδική κίνηση. Παραδείγματα περιοδικών κινήσεων είναι η κίνηση της κούνιας, η περιστροφή της γης γύρω από τον Ήλιο , η κίνηση του μυς της καρδιάς, η κίνηση του λεπτοδείκτη, η κίνηση του γιο-γιο κ.α.
Ταλάντωση
Θα προχωρήσουμε παραπέρα και θα δούμε μια υποκατηγορία περιοδικών κινήσεων και συγκεκριμένα της ταλάντωσης.

Ορισμός Ταλάντωση ονομάζουμε την περιοδική κίνηση που γίνεται πάνω στην ίδια ανοικτή γραμμή, μεταξύ δυο ακραίων θέσεων και μάλιστα γύρω από μια θέση ισορροπίας.
Παραδείγματα ταλάντωσης: Η κίνηση της κούνιας και η κίνηση του γιο – γιό είναι παραδείγματα ταλάντωσης. Η κίνηση της γης γύρω από τον Ήλιο και συγκεκριμένα κάθε κυκλική κίνηση αν και είναι περιοδικές κινήσεις δεν είναι ταλαντώσεις, διότι η τροχιά είναι κυκλική κλειστή γραμμή χωρίς να έχει μέγιστο και ελάχιστο και το σώμα δεν κινείται γύρω από μια θέση ισορροπίας,
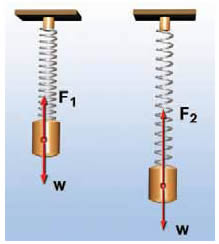
Παράδειγμα Κρεμάμε κατακόρυφα ένα ελατήριο σε ακλόνητο σημείο και στο άλλο στερεώνουμε ένα βαρίδι. Τραβάμε κατακόρυφα το βαρίδι και το αφήνουμε ελεύθερο. Παρατηρούμε ότι το σύστημα κάνει ταλάντωση. Το ελατήριο ασκεί μεταβαλλόμενη δύναμη στο βαρίδι και αυτό ταλαντώνεται. Το βαρίδι περνά από μια θέση στην οποία η συνισταμένη δύναμη είναι μηδενική. Αυτή η θέση ονομάζεται θέση ονομάζεται θέση ισορροπίας. Καθώς το βαρίδι απομακρύνεται από τη θέση ισορροπίας η συνισταμένη δύναμη τείνει να επαναφέρει το βαρίδι στη θέση ισορροπίας.
Δύναμη στην αρμονική ταλάντωση.
Κατά την ταλάντωση ενός σώματος, η συνισταμένη δύναμη σ΄ αυτό τείνει να επαναφέρει το σώμα στη θέση ισορροπίας και γιαυτό η συνισταμένη δύναμη σε ένα σώμα που κάνει ταλάντωση ονομάζεται δύναμη επαναφοράς,
Ορισμός απλής αρμονικής ταλάντωσης: Όταν η δύναμη επαναφοράς που ασκείται σε ένα σώμα είναι ανάλογη της απομάκρυνσης του σώματος από τη θέση ισορροπίας, το σώμα εκτελεί απλή αρμονική ταλάντωση.
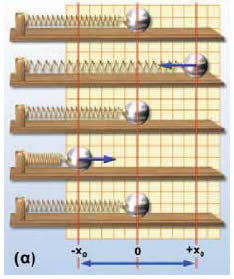
Εκτελούμε το ακόλουθο πείραμα: Στερεώνουμε το ένα άκρο του οριζόντιου ελατηρίου σε ακλόνητο σημείο και στο άλλο μια μικρή σφαίρα. Απομακρύνουμε τη σφαίρα από τη θέση ισορροπίας και έπειτα την αφήνουμε ελεύθερη. Θα αποδείξουμε ότι η μικρή σφαίρα θα εκτελέσει απλή αρμονική ταλάντωση.
Η δύναμη που ασκεί το ελατήριο στη μικρή σφαίρα είναι μια δύναμη επαναφοράς που προκαλεί την επαναφορά στη θέση ισορροπίας. Το μέτρο της δύναμης ελατηρίου σύμφωνα με το νόμο του Hooke είναι ανάλογη με τη μεταβολή του μήκους του ελατηρίου, δηλαδή με την απομάκρυνση της μικρής σφαίρας από τη θέση ισορροπίας. Πρέπει να σημειώσουμε ότι η κατεύθυνση της δύναμης επαναφοράς είναι αντίθετη με εκείνη του διανύσματος της μετατόπισης της μικρής σφαίρας από τη θέση ισορροπίας.
Ορισμός: όταν η δύναμη επαναφοράς είναι ανάλογη της απομάκρυνσης του σώματος από τη θέση ισορροπίας, τότε η κίνηση που κάνει το σώμα ονομάζεται απλή αρμονική ταλάντωση.
Μεγέθη που χαρακτηρίζουν μια ταλάντωση
Η ταλάντωση ως φυσικό φαινόμενο, περιγράφεται από τα ακόλουθα φυσικά μεγέθη: την περίοδο, την συχνότητα και το πλάτος της ταλάντωσης.
Περίοδος ταλάντωσης Σε μια ταλάντωση, η περίοδος της ταλάντωσης ορίζεται σαν το χρονικό διάστημα κατά το οποίο πραγματοποιείται μια πλήρη ταλάντωση. Εκτελούμε το ακόλουθο πείραμα: Ένα σώμα είναι κρεμασμένο σε ένα κατακόρυφο ελατήριο. Στο σώμα αρκούνται δυο δυνάμεις: η δύναμη ελατηρίου και το βάρος, που η συνταμένη τους λέγεται δύναμη επαναφοράς. Με το χέρι μας το εκτρέπουμε κατακόρυφα στη θέση Α και το αφήνουμε ελεύθερο.
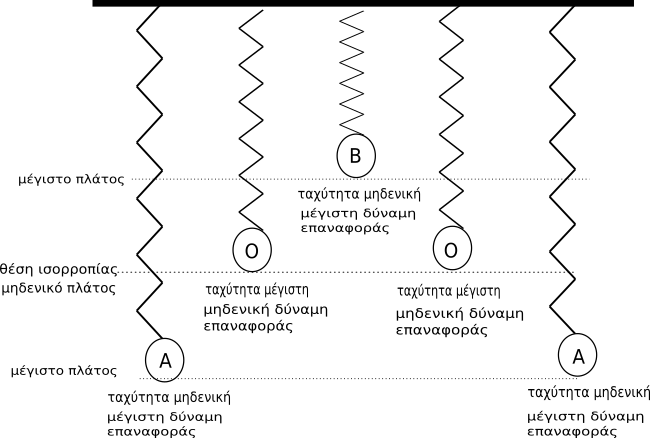
Παρατηρούμε ότι το σώμα κάνει ταλαντώσεις. Από τη θέση Α η δύναμη επαναφοράς το φέρνει προς τη θέση ισορροπίας Ο. Στη θέση ισορροπίας η δύναμη επαναφοράς είναι μηδέν, ενώ η ταχύτητα είναι μέγιστη, με αποτέλεσμα να συμπιέσει το ελατήριο στη μέγιστη θέση Β. Η δύναμη επαναφοράς αναγκάζει το σώμα να κινηθεί προς τη θέση ισορροπίας Ο και επειδή εκεί έχει τη μέγιστη ταχύτητα, έχει σαν αποτέλεσμα, η δύναμη επαναφοράς θα φέρει το σώμα στο ίδιο μέγιστο πλάτος.
Ο χρόνος που κάνει το σώμα να κινηθεί από την ακραία θέση Α στην άλλη ακραία θέση Β και μετά να επιστρέψει στη θέση Α ονομάζεται περίοδος της ταλάντωσης.
Συχνότητα ταλάντωσης Ένα σώμα που εκτελεί ταλάντωση, το οποίο μέσα σε ένα χρονικό διάστημα Δt κάνει Ν ταλαντώσεις, ορίζεται το φυσικό μέγεθος συχνότητας της ταλάντωσης ως εξής:
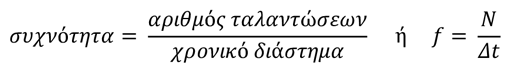
Μονάδα μέτρησης της συχνότητας στο Διεθνές Σύστημα Μονάδων είναι το 1Ηz (Χερτζ) και ορίζεται ως εξής: 1Ηz είναι η συχνότητα ενός σώματος που κάνει μια πλήρη ταλάντωση μέσα σε χρόνο ενός δευτερολέπτου (1s).
Παράδειγμα: Αν ένα σώμα ταλαντώνεται και εκτελεί 120 ταλαντώσεις σε χρόνο ενός λεπτού, η συχνότητα της ταλάντωσης είναι f=N/Δt = 120/60s = 2Hz.
Σε χρονικό διάστημα ίσο με μια περίοδο, το σώμα κάνει μια πλήρη ταλάντωση, επομένως η σχέση που συνδέει τη συχνότητα με τη περίοδο είναι f=1/T. Συνεπώς η συχνότητα f μιας ταλάντωσης είναι ίση με το αντίστροφο της περιόδου.
Πλάτος ταλάντωσης Ένα σώμα που εκτελεί ταλάντωση, φτάνει κάθε φορά σε μια από τις δυο ακραίες θέσεις, στις οποίες η απομάκρυνση από την θέση ισορροπίας είναι μέγιστη, όπου εκεί η ταχύτητα μηδενίζεται και η δύναμη επαναφοράς έχει πάρει τη μέγιστη τιμή. Η απόσταση των ακραίων θέσεων από την θέση ισορροπίας ονομάζεται πλάτος της ταλάντωσης.
Τι είναι το απλό εκκρεμές
Με τον όρο απλό εκκρεμές, εννοούμαι ένα μικρό σώμα, το οποίο είναι δεμένο στην άκρη ενός κατακόρυφου νήματος, ενώ το άλλο άκρο του είναι δεμένο σε ακλόνητο σημείο.
Όταν το σώμα ισορροπεί, τότε το νήμα έχει κατακόρυφη διεύθυνση. Μόλις απομακρύνουμε το σώμα από την κατακόρυφη θέση ισορροπίας, αυτό αρχίζει να ταλαντεύεται μεταξύ δυο ακραίων θέσεων Α και Β.
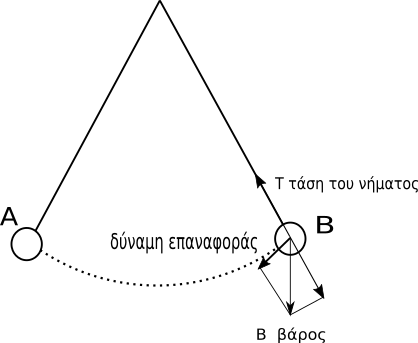
Κατά την ταλάντωση του σώματος, στο σώμα ασκούνται δυο δυνάμεις το βάρος και τάση του νήματος, που η συνισταμένη τους είναι η δύναμη επαναφοράς.
Όπως παρατηρούμε στο σχήμα η συνιστώσα του βάρους w2 τείνει να επαναφέρει το σώμα στη θέση ισορροπίας. Η μέγιστη τιμή της γωνίας ορίζει το πλάτος της ταλάντωσης.
Μεγέθη που καθορίζουν το πλάτος ταλάντωσης ενός εκκρεμούς.
Η περίοδος της ταλάντωσης ενός απλού εκκρεμούς:
α] Είναι ανεξάρτητο από τη μάζα του. Αυτό αποδεικνύεται πειραματικά αν αντικαταστήσουμε το σώμα με άλλο διαφορετικής μάζας, θα παρατηρήσουμε ότι η περίοδος παραμένει η ίδια.
β] Είναι ανεξάρτητη από το πλάτος της ταλάντωσης. Αυξάνοντας λίγο το πλάτος της ταλάντωσης, παρατηρούμε ότι η περίοδος δεν μεταβάλλεται. Αυτό ισχύει όταν εκτρέπεται κατά γωνία μικρότερη 10 μοιρών.
Γ] Εξαρτάται από το μήκος του νήματος. Αν αυξήσουμε το μήκος του νήματος θα παρατηρήσουμε ότι η περίοδος της ταλάντωσης αυξάνει.
Συμπέρασμα: Δυο εκκρεμή με ίδιο μήκος θα έχουν την ίδια περίοδο ταλάντωσης, ανεξάρτητα από το πλάτος και της μάζας τους. Βάση αυτής της ιδιότητας του απλού εκκρεμές, βασίζεται η κατασκευή χρονομετρικού εκκρεμούς.
Η περίοδος ενός απλού εκκρεμούς αλλάζει με την επιτάχυνση της βαρύτητας στον τόπο που βρίσκεται. Το απλό εκκρεμές στον ισημερινό της Γης έχει μεγαλύτερη περίοδο ταλάντωσης από το ίδιο αν βρεθεί στους πόλους της Γης. Στη Σελήνη η περίοδος ταλάντωσης του ίδιου εκκρεμούς αυξάνεται κατά τα 2,5 φορές περίπου.
Ενέργεια και ταλάντωση
Ένα σώμα που κάνει ταλάντωση, όπως ένα σώμα στερεωμένο σε ένα ελατήριο, σ’ αυτό ασκείται δύναμη επαναφοράς, που τείνει να φέρει το σώμα στη θέση ισορροπίας. Για να θέσουμε σε ταλάντωση ένα σώμα που είναι στερεωμένο σε ελατήριο, του ασκούμε δύναμη με το χέρι μας, μέχρι να φτάσει σε μια (μέγιστη) απόσταση, από τη θέση ισορροπίας και το αφήνουμε ελεύθερο. Η δύναμη του χεριού μας παράγει έργο, οπότε στο σώμα προσφέρεται ενέργεια. Η ενέργεια αυτή αποθηκεύεται με τη μορφή της δυναμικής ενέργειας.
Ποιες ενεργειακές μεταβολές συμβαίνουν κατά την ταλάντωση;
Για να μπορέσουμε να θέσουμε ένα σώμα σε ταλάντωση (σώμα + ελατήριο) πρέπει σ’ αυτό να ασκηθεί αρχικά μια επιπρόσθετη δύναμη που θα το απομακρύνει από τη θέση ισορροπίας του. Η δύναμη αυτή μέσου του έργου που παράγει, προσφέρει ενέργεια στο σώμα, η οποία αποθηκεύεται με τη μορφή δυναμικής ενέργειας.
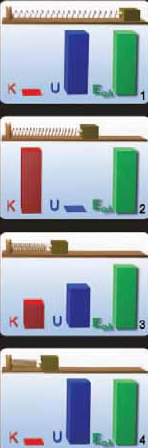
Στην διπλανή εικόνα φαίνονται τα διαδοχικά στιγμιότυπα της ταλάντωσης. Στο (1) το σώμα έχει φτάσει στη μέγιστη απομάκρυνση, η οποία το σώμα έχει μηδενική ταχύτητα και συνεπώς μηδενική κινητική ενέργεια καθώς και μέγιστη δυναμική ενέργεια.
Έπειτα το σώμα κινείται προς τη θέση ισορροπίας στην οποία η παραμόρφωση του ελατηρίου μικραίνει και συνεπώς η δυναμική ενέργεια του σώματος μειώνεται. Σε αυτή την κίνηση η ταχύτητα του σώματος αυξάνει όπως και η κινητική ενέργεια του. Στη θέση ισορροπίας (2) η κινητική ενέργεια γίνεται μέγιστη ενώ η δυναμική γίνεται μηδέν.
Έπειτα καθώς το σώμα απομακρύνεται από τη θέση ισορροπίας και κατευθύνεται στο άλλο άκρο μέγιστης απομάκρυνσης, (3) αυξάνεται η δυναμική του ενέργεια ενώ η κινητική του ενέργεια ελαττώνεται.
Στη θέση της μέγιστης απομάκρυνσης (4) η κινητική ενέργεια γίνεται μηδέν, ενώ η δυναμική ενέργεια μεγιστοποιείται.
Συμπέρασμα: Σε μια ταλάντωση πραγματοποιείται περιοδικά μετατροπή της δυναμικής ενέργειας σε κινητική και αντίστροφα.
Στις πραγματικές ταλαντώσεις, το πλάτος της ταλάντωσης μειώνεται σταδιακά μέχρι να ακινητοποιηθεί το σώμα. Αυτό οφείλεται στο γεγονός ότι υπάρχουν δυνάμεις τριβής ή δυνάμεις αντίστασης του αέρα.
Ένα παράδειγμα ταλάντωσης με επίδραση τριβών είναι η κούνια, η οποία η κίνηση της σταματά αργότερα με την επίδραση τριβών ή την αντίσταση του αέρα.
Στην ιδανική περίπτωση που δεν υπάρχουν δυνάμεις τριβής, η μηχανική ενέργεια της ταλάντωσης, δηλαδή το άθροισμα της κινητικής (Κ) και της δυναμικής ενέργειας (U) διατηρείται σταθερό.
Κ + U = Ε = σταθερό
Η μηχανική ενέργεια ενός σώματος που εκτελεί ταλάντωση (Δυναμική + Κινητική ενέργεια) διατηρείται σταθερή και αυτό στην ιδανική περίπτωση που δεν έχουμε τριβές. Όμως σε μια πραγματική ταλάντωση όπως στην περίπτωση της κούνιας, υπάρχουν αντιστάσεις που μετατρέπουν τη μηχανική ενέργεια σε θερμική. Έτσι με τη σταδιακή μείωση της μηχανικής ενέργειας έχουμε μείωση στο πλάτος της ταλάντωσης και έτσι η κούνια σε λίγο χρόνο σταματά.
Η κούνια θα μπορεί να ταλαντεύεται συνεχώς μόνο όταν παρέχουμε σε αυτή με κατάλληλο τρόπο ενέργεια, ώστε να αναπληρώνεται η μηχανική ενέργεια που μετατρέπεται σε θερμική λόγω τριβών.