Η έννοια της πίεσης

Είπαμε σε προηγούμενη ενότητα ότι ένα αποτέλεσμα μιας δύναμης είναι η παραμόρφωση του σώματος στο οποίο ενεργεί. Για να περιγράψουμε το μέγεθος της παραμόρφωσης πρέπει να λάβουμε υπόψη κι ένα άλλο παράγοντα, το εμβαδόν στο οποίο εφαρμόζεται η δύναμη.

Ας πάρουμε για παράδειγμα ένα άνδρα που στέκεται στο χιόνι. Αν φοράει χιονοπέδιλα δεν βουλιάζει στο χιόνι και μπορεί να κινηθεί σ’ αυτό, σε αντίθεση μ’ αυτόν που φοράει μόνο τα παπούτσια του, που βουλιάζει στο χιόνι και δεν μπορεί να κινηθεί. Σε κάθε περίπτωση ο άνδρας ασκεί την ίδια δύναμη στο χιόνι, το βάρος του, αλλά όταν φοράει χιονοπέδιλα αυτή η δύναμη κατανέμεται σε μεγάλη επιφάνεια και λέμε ότι έχουμε μικρή πίεση, σε αντίθεση που όταν φορά τα παπούτσια του που το βάρος του κατανέμεται σε μικρή επιφάνεια, οπότε λέμε ότι έχουμε μεγάλη πίεση.

Ένα άλλο παράδειγμα είναι όταν καρφώνουμε σε ένα κομμάτι ξύλο μια πινέζα. Η δύναμη που ασκούμε στο κεφάλι της πινέζας είναι η ίδια με τη δύναμη που ασκεί η πινέζα στο ξύλο. Αλλά επειδή το κεφάλι της πινέζας έχει πολύ μεγαλύτερο εμβαδόν από τη μύτη της, λέμε ότι η πίεση στο κεφάλι είναι μικρή ενώ η πίεση στη μύτη είναι μεγάλη. Γι’ αυτό το λόγο το ξύλο παραμορφώνεται και εισχωρεί η πινέζα στο ξύλο και δεν έχουμε πρόβλημα με την πίεση που ασκούμε με το χέρι μας στο κεφάλι της πινέζας.

Από τα παραπάνω παραδείγματα καταλαβαίνουμε ότι όσο πιο μικρή είναι η επιφάνεια πάνω στην οποία ενεργεί μια δύναμη, τόσο μεγαλύτερη είναι η ικανότητα της να προκαλέσει παραμόρφωση. Αυτή η ικανότητα της δύναμης εκφράζεται με το φυσικό μέγεθος της πίεσης.

Ορισμός: Όταν μια δύναμη μέτρου F ενεργεί ομοιόμορφα και κάθετα σε μια επιφάνεια Α ορίζουμε το φυσικό μέγεθος πίεση, ως το πηλίκο της δύναμης F προς την επιφάνεια Α:

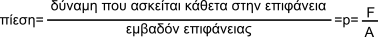
Η μονάδα πίεσης στο Διεθνές Σύστημα Μονάδων είναι το Pascal (Pa) που ορίζεται ως εξής: 1 Pa (πασκάλ) είναι η πίεση που δημιουργεί μια δύναμη μέτρου 1Ν αν ενεργήσει κάθετα σε μια επιφάνεια 1m²

Επειδή η πίεση ίση με 1 Pa είναι πολύ μικρή χρησιμοποιούμε το πολλαπλάσιο της το 1kPa (κιλοπασκάλ) = 10³Pa = 1000Pa.

Η κυριότερη διαφορά της πίεσης από τη δύναμη είναι ότι η πίεση είναι μονόμετρο μέγεθος ενώ η δύναμη είναι διανυσματικό μέγεθος.

Πίεση των ρευστών

Ρευστά ονομάζουμε τα σώματα που δεν έχουν σταθερό σχήμα, αλλά αποκτούν το σχήμα του δοχείου που τα περιέχει. Ονομάζονται ρευστά λόγω της ιδιότητας τους να ρέουν. Ρευστά είναι τα υγρά και τα αέρια.

Κάθε ρευστό που βρίσκεται σε ισορροπία, ασκεί στα τοιχώματα των σωμάτων που βρίσκεται σε επαφή δύναμη και επομένως ασκεί πίεση σ’ αυτά. Η πίεση που ασκεί ένα υγρό που ισορροπεί ονομάζεται υδροστατική πίεση, ενώ η πίεση που ασκείται από τον ατμοσφαιρικό αέρα ονομάζεται ατμοσφαιρική πίεση.

Υδροστατική πίεση

Η έννοια της υδροστατικής πίεσης

Που οφείλεται η υδροστατική πίεση: Σε ένα υγρό που ισορροπεί σε ένα δοχείο ασκούνται δυο δυνάμεις: το βάρος του w και η δύναμη F_N  που δέχεται το υγρό από το πυθμένα. Αυτές οι δυο δυνάμεις έχουν συνισταμένη μηδέν, οπότε για τα μέτρα τους έχουμε:

F_N=w

Ας γράψουμε ότι το υγρό θα ασκεί δύναμη F’_N στο πυθμένα του δοχείου. Η δύναμη F’_N που ασκεί το υγρό στο πυθμένα με τη δύναμη F_N που δέχεται το υγρό από τον πυθμένα θα έχουν σχέση δράσης – αντίδρασης, άρα το μέτρο της δύναμης που ασκεί το υγρό στο πυθμένα θα είναι ίσο με το βάρος του. Οπότε η πίεση του υγρού στον πυθμένα είναι ίση με:

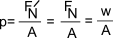
Συμπερένουμε λοιπόν ότι η υδροστατική πίεση των υγρών οφείλεται στο βάρος τους. Ας κάνουμε το παρακάτω νοητό πείραμα: Έστω η υδροστατική πίεση ενός υγρού σε ένα δοχείο που βρίσκεται στη Γη έχει μια τιμή. Αν μεταφέρουμε το δοχείο στη Σελήνη, η υδροστατική πίεση θα μειωθεί κατά 6 φορές. Πράγματι επειδή η δύναμη βαρύτητας στη Σελήνη είναι 6 φορές μικρότερη από εκείνη στη Γη, από τον τύπο p=w/A αποδεικνύεται ο ισχυρισμός μας.

Μέτρηση της υδροστατικής πίεσης

Για να μετρήσουμε την υδροστατική πίεση ενός υγρού, χρησιμοποιούμαι ειδικά όργανα τα μανόμετρα. Ένας απλός τύπος μανομέτρου που χρησιμοποιούμε στο εργαστήριο της φυσικής, αποτελείται από ένα διαφανές σωλήνα σε σχήμα U ο οποίος περιέχει κάποιο υγρό π.χ. υδράργυρο ή λάδι. Το ένα σκέλος του σωλήνα συνδέεται με ελαστικό σωλήνα ο οποίος η άλλη του άκρη τερματίζεται σε μια κάψα που στην μια της μεριά κλείνεται με ελαστική μεμβράνη. Η κάψα τοποθετείται στο υγρό στο σημείο που θέλουμε να μετρήσουμε την υδροστατική πίεση. Η μεμβράνη παραμορφώνεται και πιέζει τον αέρα που βρίσκεται μέσα στον ελαστικό σωλήνα. Ο αέρας του ελαστικού σωλήνα πιέζει το υγρό του μανομέτρου, οπότε δημιουργείται υψομετρική διαφορά στο υγρό των δυο σκελών του μανομέτρου. Η διαφορά της στάθμης στα δυο σκέλη είναι η ένδειξη του μανομέτρου που είναι ανάλογης της υδροστατικής πίεσης που δέχεται η κάψα.

Όσο μεγαλύτερη είναι η πίεση του υγρού τόσο περισσότερο παραμορφώνεται η μεμβράνη και τόσο περισσότερο μεγαλώνει η διαφορά στάθμης στα δυο σκέλη του μανομέτρου.

Νόμος της υδροστατικής πίεσης

Στην αρχή της ενότητας είπαμε ότι η υδροστατική πίεση ενός υγρού οφείλεται στο βάρος του. Στη συνέχεια θα αναζητήσουμε πως συνδέεται η υδροστατική πίεση με τα άλλα φυσικά μεγέθη που έχει σχέση. Για να το πετύχουμε αυτό κάνουμε μια σειρά πειραμάτων.

Υδροστατική πίεση και βάθος Για να συσχετίσουμε την υδροστατική πίεση με το βάθος, καταφεύγουμε στο πείραμα. Τοποθετούμε την μανομετρική κάψα σε διάφορα βάθη και μετράμε την πίεση με το μανόμετρο. Με επεξεργασία των μετρήσεων ανακαλύπτουμε ότι η υδροστατική πίεση αυξάνεται ανάλογα με το βάθος.

Υδροστατική πίεση και πυκνότητα του υγρού Για να βρούμε τη σχέση της υδροστατικής πίεσης με την πυκνότητα του υγρού εκτελούμε το παρακάτω πείραμα: Παίρνουμε δυο δοχεία το ένα με καθαρό οινόπνευμα το οποίο έχει πυκνότητα ρ_οιν=800Kg/m³ και το άλλο με αλατόνερο το οποίο έχει πυκνότητα ρ_αλ=1600Kg/m³. Μετράμε με το μανόμετρο την υδροστατική πίεση, στο ίδιο βάθος, και βρίσκουμε ότι η υδροστατική πίεση στο δοχείο με το αλατόνερο είναι διπλάσια από εκείνη στο δοχείο με το οινόπνευμα. Με αυτό το πείραμα και καθώς με άλλα συμπεραίνουμε ότι η υδροστατική πίεση είναι ανάλογη με την πυκνότητα του υγρού.

Νόμος της υδροστατικής πίεσης Με τα παραπάνω πειραματικά δεδομένα καθώς και με την εκτέλεση άλλων πειραμάτων, καταλήγουμε στο ότι η υδροστατική πίεση είναι ανάλογη με:
1] Με το βάθος από την επιφάνεια του υγρού.
2] Με την πυκνότητα του υγρού.
3] Με την επιτάχυνση της βαρύτητας.

Τα παραπάνω συμπεράσματα εκφράζονται με τη γλώσσα των μαθηματικών με την παρακάτω σχέση, που λέγεται νόμος της υδροστατικής πίεσης:

p = ρ ∙ g ∙ h

Όπου p η υδροστατική πίεση σε Ν/m² , ρ η πυκνότητα του υγρού σε Κg/m³ , g η επιτάχυνση της βαρύτητας σε m/s² και h το βάθος από την επιφάνεια του υγρού σε m.

Απλή απόδειξη του νόμου της υδροστατικής πίεσης. Θεωρούμε ότι έχουμε ένα κυλινδρικό δοχείο με εμβαδόν βάσης Α και ότι έχει ύψος h, το οποίο είναι γεμάτο με υγρό πυκνότητας ρ. Ο όγκος του υγρού που περιέχει είναι ίσος με V = A ∙ h ενώ η μάζα του θα είναι m = ρ ∙ V = ρ ∙ Α ∙ h

Το βάρος του υγρού εκφράζεται με τη σχέση w = m ∙ g = ρ ∙ Α ∙ h ∙ g

Επειδή το υγρό ισορροπεί θα δέχεται δύναμη F από το πυθμένα κατά μέτρο ίση με το βάρος του w δηλαδή F = w. Λόγω του τρίτου νόμου του Νεύτωνα, δηλαδή της σχέσης δράσης – αντίδρασης, το υγρό θα ασκεί στο πυθμένα δύναμη F’ με μέτρο ίσο της δύναμης F, δηλαδή:
F’ = F = w  και  συγκεκριμένα   F’ = ρ ∙ Α ∙ h ∙ g

Η πίεση στο πυθμένα λόγω της δύναμης F’ που ασκεί το υγρό στο πυθμένα, θα είναι:

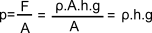
Δηλαδή, η υδροστατική πίεση p υγρού πυκνότητας ρ σε βάθος h από την ελεύθερη επιφάνεια του υγρού εκφράζεται ως: (g η επιτάχυνση της βαρύτητας)

p = ρ ∙ h ∙ g

Υδροστατική πίεση είναι ανεξάρτητη από τον όγκο και το σχήμα του δοχείου.

Εκτελούμε το παρακάτω πείραμα: Έχουμε διάφορα δοχεία από το ίδιο υγρό τα οποία περιέχουν διαφορετική ποσότητα του ίδιου υγρού. Βάζουμε τη μανομετρική κάψα σε καθένα από τα δοχεία και στο ίδιο βάθος και μετράμε την υδροστατική πίεση. Παρατηρούμε ότι η υδροστατική πίεση είναι ίδια για το ίδιο βάθος ανεξάρτητη από το σχήμα του δοχείου και τη μάζα του υγρού.

Συγκοινωνούντα δοχεία

Από το νόμο της υδροστατικής πίεσης προκύπτει ότι σε δυο διαφορετικά σημεία του υγρού που βρίσκονται στο ίδιο βάθος από την ελεύθερη επιφάνεια του υγρού έχουν την ίδια πίεση. Αυτή η αρχή εφαρμόζεται στα συγκοινωνούντα δοχεία. Συγκοινωνούντα δοχεία λέμε διάφορα δοχεία με διαφορετικό σχήμα και μέγεθος που συνδέονται μεταξύ τους με ένα σωλήνα στο κατώτερο σημείο τους, όπως βλέπουμε στο σχήμα.

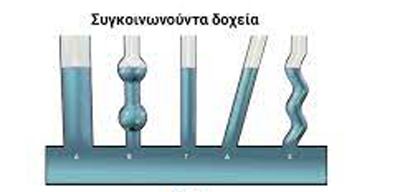
Αν ρίξουμε υγρό σε ένα από αυτά, μέσω του σωλήνα θα διοχετευτεί υγρό και στα υπόλοιπα δοχεία. Παρατηρούμε ότι όταν επέλθει ισορροπία η στάθμη του υγρού είναι στο ίδιο επίπεδο για όλα τα δοχεία. Αν σε ένα δοχείο η στάθμη ήταν υψηλότερη από τα υπόλοιπα θα είχαμε διαφορετική υδροστατική πίεση στον πυθμένα και θα είχαμε κίνηση του υγρού, πράγμα που δεν συμβαίνει, άρα η στάθμη του υγρού στα συγκοινωνούντα δοχεία είναι στο ίδιο επίπεδο.

Την αρχή των συγκοινωνούντων δοχείων την εκμεταλλευόμαστε στο σύστημα υδροδότησης των πόλεων. Συγκεκριμένα οι δεξαμενές ύδρευσης κατασκευάζονται στα ψηλότερα σημεία των πόλεων έτσι ώστε λόγω της διαφοράς της υδροστατικής πίεσης το νερό να κινείται μέσω σωληνώσεων και να φτάνει στους υψηλότερους ορόφους των σπιτιών χωρίς να χρειάζεται τη χρήση αντλιών.

Μέτρηση της ατμοσφαιρικής πίεσης

Η έννοια της ατμοσφαιρικής πίεσης

Η ατμοσφαιρική πίεση μετρήθηκε για πρώτη φορά το 1643 από το φυσικό Εβαγγελίστα Τορικέλι. Ο Τορικέλι πήρε ένα γυάλινο σωλήνα μήκους 1m, κλειστό από την μια μεριά και τον γέμισε με υδράργυρο. Έπειτα έκλεισε το στόμιο του με το δάκτυλο του και τον αναποδογύρισε σε μια λεκάνη με υδράργυρο και στη συνέχεια άφησε ελεύθερο το άκρο του. Ο Τορικέλι παρατήρησε ότι το ύψος του υδραργύρου στο σωλήνα μειώθηκε φτάνοντας στο ύψος 76cm από την επιφάνεια της λεκάνης με τον υδράργυρο.

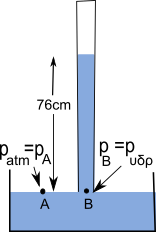
Ερώτηση: Γιατί ο υδράργυρος στον σωλήνα δεν άδειασε όλος στη λεκάνη; Απάντηση: Θεωρούμε δυο σημεία Α και Β όπου το Α το παίρνουμε στην επιφάνεια του υδραργύρου της λεκάνης και το άλλο σημείο Β το παίρνουμε στη βάση μέσα στο σωλήνα υδραργύρου στο ίδιο ύψος με το σημείο Α. Σύμφωνα με την αρχή των συγκοινωνούντων δοχείων, η πίεση στα σημεία Α και Β είναι η ίδια, δηλαδή:

p_A = p_B

Η πίεση στο σημείο Α είναι η ατμοσφαιρική πίεση p_A=p_atm ενώ η πίεση στο σημείο Β είναι η υδροστατική πίεση που προκαλεί η στήλη υδραργύρου του σωλήνα: p_B=p_υδρ  Συγκρίνοντας τις παραπάνω σχέσεις προκύπτει ότι η ατμοσφαιρική πίεση είναι ίση με την πίεση που ασκεί στη βάση η στήλη υδραργύρου με ύψος 76cm (όταν εκτελείται το πείραμα στην επιφάνειά της θάλασσας). Έτσι η ατμοσφαιρική πίεση δεν αφήνει τον υδράργυρο του σωλήνα να χυθεί στην λεκάνη.

Την υδροστατική πίεση που ασκεί στήλη υδραργύρου ύψους 1 mm την ονομάζουμε 1 Torr προς τιμήν του Τορικέλι. Επομένως η ατμοσφαιρική πίεση στην επιφάνεια της θάλασσας ισούται με 760 Torr.

Για τη μέτρηση της ατμοσφαιρικής πίεσης χρησιμοποιούμε όργανα που ονομάζονται βαρόμετρα.

Πως υπολογίζουμε την ατμοσφαιρική πίεση

Η ατμοσφαιρική πίεση είναι ίση με την υδροστατική πίεση μιας στήλης υδραργύρου ύψους h και συνεπώς υπολογίζεται από τον τύπο:

p_atm = p_υδρ = ρ ∙ g ∙ h

Γνωρίζουμε την πυκνότητα του υδραργύρου που έχει τιμή ρ=13.600kg/m³ , την επιτάχυνση της βαρύτητας στην επιφάνεια της θάλασσας που έχει τιμή g=9,8m/s², ενώ το ύψος της στήλης υδραργύρου στο σωλήνα έχει τιμή h=76cm=0,76m. Με αντικατάσταση των τιμών στην παραπάνω σχέση παίρνουμε:

p_atm = 13.600Kg/m³ ∙ 9,8m/s² ∙ 0,76m  ή   p_atm = 101.293Pa  (πασκάλ)

Έτσι υπολογίσαμε ότι η πίεση μιας ατμόσφαιρας είναι ίση με 101.293Pa. Αν δεν θέλουμε μεγάλη ακρίβεια γράφουμε 1atm = 100.000Pa. Σημείωση: πίεση μιας ατμόσφαιρας είναι ίση με την ατμοσφαιρική πίεση στην επιφάνεια της θάλασσας.

Δυνάμεις λόγω ατμοσφαιρικής πίεσης

Λόγω της ατμοσφαιρικής πίεσης τα σώματα που βρίσκονται μέσα στον αέρα δέχονται τεράστιες δυνάμεις. Λόγω της ατμοσφαιρικής πίεσης στο ανθρώπινο σώμα ασκούνται δυνάμεις της τάξης των 100.000Ν. Όμως οι δυνάμεις αυτές δεν συνθλίβουν το ανθρώπινο σώμα διότι η πίεση στο εσωτερικό του σώματος είναι ίση με την ατμοσφαιρική πίεση.

Αν με ένα καλαμάκι αφαιρέσουμε τον αέρα από ένα χάρτινο κουτί πορτοκαλάδας, η εξωτερική δύναμη που ασκεί ο ατμοσφαιρικός αέρας προκαλεί την παραμόρφωση του κουτιού.

Για να καταφέρουμε να πιούμε το αναψυκτικό μας χρησιμοποιούμε ένα καλαμάκι. Καθώς ρουφούμε τον αέρα και το υγρό που υπάρχει στο καλαμάκι, έχει ως αποτέλεσμα η δύναμη που ασκεί η ατμοσφαιρική πίεση στην επιφάνεια του αναψυκτικού αναγκάζει το αναψυκτικό να ανέβει στο στόμα μας. Στη Σελήνη όπου δεν υπάρχει ατμοσφαιρική πίεση, δεν μπορούμε να πιούμε το αναψυκτικό με το καλαμάκι.