Εισαγωγή

Με τον όρο φυσικές επιστήμες εννοούμε τις ερευνητικές δραστηριότητες των επιστημόνων πάνω στη φύση και συγκεκριμένα με αυτό τον όρο ορίζουμε την μέθοδο που χρησιμοποιούν και την γνώση που έχουν αποκτήσει, κατά τη μελέτη των μεταβολών που συμβαίνουν γύρω στη φύση.

Στις φυσικές επιστήμες συγκαταλέγονται μεταξύ άλλων η φυσική, η χημεία, η βιολογία και η γεωλογία. Κάθε φυσική επιστήμη έχει το χαρακτηριστικό πεδίο ασχολίας και χρησιμοποιεί την δική της μεθοδολογία.

Οι μεταβολές που συμβαίνουν στη φύση, σε επιστημονικούς όρους ονομάζονται φαινόμενα. Η φυσική καταπιάνεται με τα φυσικά φαινόμενα, ενώ η χημεία με τα χημικά φαινόμενα. Φυσικά φαινόμενα είναι εκείνα στα οποία δεν αλλάζει η χημική σύσταση των σωμάτων που μετέχουν σ’ αυτά, ενώ χημικά φαινόμενα είναι εκείνα στα οποία αλλάζει η χημική σύσταση των σωμάτων που μετέχουν σ’ αυτά. Παραδείγματα φυσικών φαινομένων είναι ο βρασμός του νερού, η κίνηση της Σελίνης γύρω από τη γη, η κίνηση του νερού στις σωληνώσεις, ενώ χημικά φαινόμενα είναι η καύση του ξύλου καθώς και των άλλων καυσίμων σωμάτων καθώς και το σκούριασμα των σιδερένιων αντικειμένων κ.ά. Η βιολογία είναι η επιστήμη που ασχολείται με τη μελέτη των φαινομένων που σχετίζονται με τη ζωή. Τέλος η γεωλογία είναι η επιστήμη που μελετά τη μορφολογία και τη σύσταση του εδάφους και ερευνά τους μηχανισμούς με τους οποίους διαμορφώνεται το έδαφος.

Οι επιστήμονες προσπαθούν διαρκώς να κατανοήσουν τους μηχανισμούς με τους οποίους λειτουργεί η φύση και με  αυτό τον τρόπο να μπορούν να προβλέπουν και να ελέγχουν τα φαινόμενα (μεταβολές της φύσης).

Φυσική μια θεμελιώδης επιστήμη.

Η φυσική είναι η βάση των άλλων φυσικών επιστημών, αφού παρέχει τις θεμελιώδης γνώσεις για τη δομή της ύλης και της λειτουργίας της, οι οποίες είναι αναγκαίες για την ανάπτυξη και των άλλων φυσικών επιστημών.

Επίσης γνωρίζοντας τους βασικούς νόμους της φυσικής, μπορεί ο καθένας μας, να κατανοήσει τα φαινόμενα που συμβαίνουν γύρω μας π.χ. για το πως δημιουργούνται οι σεισμοί, που βασίζεται η λειτουργία του πυρηνικού αντιδραστήρα κ.ά., πως λειτουργούν οι συσκευές που χρησιμοποιούμε στη καθημερινή ζωή, όπως π.χ. ο ηλεκτρονικός υπολογιστής, το κινητό τηλέφωνο, η τηλεόραση, το ηλεκτρικό ψυγείο, ο φούρνος μικροκυμάτων και απαντήσει σε απορίες όπως π.χ. πως σχηματίζεται το ουράνιο τόξο, πως δημιουργούνται οι κεραυνοί και οι αστραπές, γιατί τα αστέρια λάμπουν στον ουρανό, πως οι δορυφόροι περιστρέφονται γύρω από τη γή κ.ά.

Οι φυσικοί παρατηρούν με προσοχή τη φύση, αναζητώντας ομοιότητες των φαινομένων και εκτελώντας πειράματα προσπαθούν να ανακαλύψουν τους βαθύτερους νόμους που κυβερνούν τη φύση και στόχος τους είναι να τους διατυπώνουν με τη μεγαλύτερη δυνατή ακρίβεια, σαφήνεια και απλότητα. Έτσι οι φυσικοί επιστήμονες προσπαθούν να αναπτύξουν μια θεωρία που περιγράφει με απλότητα και πληρότητα όλα τα φυσικά φαινόμενα που συμβαίνουν στο σύμπαν και μάλιστα με ένα ενιαίο σύνολο εννοιών με το ίδιο νόημα με καθολικό χαρακτήρα σε όλη τη έκταση της δράσης της φυσικής. Δυο τέτοιες έννοιες είναι η ενέργεια και η αλληλεπίδραση (δήναμη).

Στη φυσική δεχόμαστε ότι τόσο στο μακρόκοσμο (γαλαξίες, αστέρια, πλανήτες) όσο και στο μικρόκοσμο (ηλεκτρόνια, νουκλεόνια, άτομα, μόρια) τα υλικά σωματίδια και σώματα αλληλεπιδρούν μεταξύ τους, που στη γλώσσα της φυσικής λέμε ότι αλληλεπιδρούν δηλαδή ασκούν δυνάμεις το ένα στο άλλο.

Η ενέργεια είναι εκείνο το φυσικό μέγεθος που χρησιμοποιούν οι φυσικοί για να περιγράψουν με ποσοτικό τρόπο τις μεταβολές που συμβαίνουν στη φύση. Στη φυσική λέμε ότι ένα σώμα περικλείει ενέργεια όταν μπορεί να προκαλέσει μεταβολές. Π.χ. Ο άνεμος περιέχει αιολική ενέργεια διότι μπορεί να θέσει σε κίνηση ένα ανεμόμυλο. Η ενέργεια παρουσιάζεται με διάφορες μορφές όπως κινητική, δυναμική, χημική, πυρηνική, αιολική και άλλες μορφές. Η ενέργεια μπορεί  να εκφραστεί ποσοτικά και υπακούει στην αρχή διατήρησης της ενέργειας, όπου σε κάθε φυσική μεταβολή το συνολικό ποσό της ενέργειας παραμένει σταθερό. Επίσης η ενέργεια δεν παράγεται από το μηδέν, ούτε εξαφανίζεται, ενώ έχει το χαρακτηριστικό γνώρισμα να μετατρέπεται από τη μια μορφή στην άλλη.

Κάθε υλικό σώμα που βρίσκεται γύρω μας στο περιβάλλον γίνεται αντιληπτό με τις αισθήσεις μας ενώ με τη βοήθεια της φυσικής «επεκτείνουμε» τις αισθήσεις μας και καταφέρνουμε να αντιληφθούμε ότι κάθε σώμα αποτελείται από ένα πλήθος μικροσκοπικών σωματιδίων οργανωμένα σε άτομα και στη συνέχεια ως μόρια, που στο σύνολο τους αποτελούν το σώμα. Σήμερα οι φυσικοί ερευνούν και προσπαθούν να απαντήσουν σε ερωτήματα που αφορούν την δομή της ύλης: «Πόσα διαφορετικά είδη τέτοιων σωματιδίων υπάρχουν;», «Ποιες οι ιδιότητες τους;» «Πως αλληλεπιδρούν μεταξύ τους;». Γενικά η φυσική είναι η επιστήμη που μελετά τις ιδιότητες των σωμάτων μικρών ή μεγάλων, δηλαδή τόσο στο μικρόκοσμο όπως στα άτομα και μόρια, όσο στο μακρόκοσμο όπως τους γαλαξίες. Η φυσική μελετά τον χώρο, τον χρόνο, την ύλη και την ενέργεια και τον τρόπο που αυτά συσχετίζονται.

Η γλώσσα της φυσικής

Οι φυσικοί κατά την περιγραφή και μελέτη των φυσικών φαινομένων, χρησιμοποιούν τη γλώσσα της φυσικής, η οποία έχει το δικό της λεξιλόγιο όπως για παράδειγμα τους όρους «χώρος», «χρόνος», «αλληλεπίδραση», «ενέργεια» κ.ά. Οι φυσικοί προσπαθούν να βρουν τις σχέσεις που συνδέουν τις έννοιες αυτές, αναπτύσσοντας τους νόμους της φυσικής. Πολλές φορές, οι όροι στο λεξιλόγιο της φυσικής είναι δανεισμένες από το λεξιλόγιο μας δηλαδή τις λέξεις της καθημερινής ζωής, αλλά στη φυσική αποκτούν άλλο νόημα.

Η φυσική είναι μια αυστηρή επιστήμη που κατάφερε να αναπτυχθεί ραγδαία μετά την επιστημονική επανάσταση τον 17^ο αιώνα κατά την οποία θεμελιώθηκε η σύγχρονη επιστημονική μέθοδος. Η επιστημονική μέθοδος βασίζεται στο πείραμα και χρησιμοποιεί τα μαθηματικά πάνω στη μελέτη των φυσικών φαινομένων και κατορθώνει να διατυπώνει τους νόμους της φυσικής χρησιμοποιώντας μαθηματικές εξισώσεις και γραφικές παραστάσεις.

Φυσικές επιστήμες και τεχνολογία

Με τον όρο τεχνολογία εννοούμε το σύνολο των πρακτικών εφευρέσεων του ανθρώπου που έδωσαν ώθηση στην ανάπτυξη κατασκευών, με σκοπό την βελτίωση της ζωής του. Παρατηρείται ότι η τεχνολογία έχει αυτοδύναμη ανάπτυξη που έχει ως θεμέλιο τη φυσική επιστήμη. Παραδείγματα τεχνολογίας είναι ο ηλεκτρονικός υπολογιστής, το κινητό τηλέφωνο, η τηλεόραση που αναπτύχθηκαν από τους επιστήμονες στηριζόμενοι στους νόμους της φυσικής και συγκεκριμένα στη φυσική ημιαγωγών, του ηλεκτρομαγνητισμού κ.ά. Από την άλλη η εξέλιξη της τεχνολογίας επιτρέπει την διεξαγωγή πολύπλοκων και ακριβή πειραμάτων της φυσικής για την ανακάλυψη των βαθύτερων νόμων της φυσικής. Έτσι βλέπουμε ότι υπάρχει μια αλληλεπίδραση μεταξύ τεχνολογίας και φυσικών επιστημών. Τέλος πρέπει να επισημάνουμε  ότι οι αρνητικές πλευρές της σύγχρονης τεχνολογίας όπως τα απόβλητα, τα καυσαέρια, οι ακτινοβολίες, δεν ευθύνεται η φυσική επιστήμη, αλλά όλοι εμείς οι άνθρωποι που δεν διαχειριζόμαστε ορθά τις γνώσεις μας.

Η επιστημονική μέθοδος

Οι φυσικοί μελετούν τα φυσικά φαινόμενα με συγκεκριμένη μεθοδολογία που ονομάζεται επιστημονική μέθοδος. Η επιστημονική μέθοδος αναπτύχθηκε στην διάρκεια πολλών αιώνων και είναι αποτέλεσμα δουλειάς πολλών ανθρώπων. Πατέρας της επιστημονικής μεθόδου είναι ο Γαλιλαίος και είναι σήμερα αποδεκτή από όλους τους επιστήμονες. Η επιστημονική μέθοδος έχει συγκεκριμένα βήματα:

1. Παρατήρηση από τους επιστήμονες ενός φαινομένου που συμβαίνει γύρω μας. Εδώ οι επιστήμονες αναζητούν τις συσχετίσεις των δεδομένων του φαινομένου.
2. Υπόθεση είναι μια προσωρινή πρόβλεψη που κάνει ο επιστήμονας βασιζόμενος στις παρατηρήσεις.
3. Πείραμα γίνεται για την επαλήθευση ή την απόρριψη της υπόθεσης που έγινε. Στο πείραμα γίνεται αναπαραγωγή του φυσικού φαινομένου κάτω σε ελεγχόμενες συνθήκες. Κατά τη διάρκεια του πειράματος κάνουμε προσεκτικές και ακριβής μετρήσεις ώστε να περιγράψουμε με πληρότητα το φυσικό φαινόμενο. Επίσης οι συνθήκες του πειράματος πρέπει να είναι απόλυτα γνωστές έτσι ώστε το πείραμα να μπορεί να επαναληφθεί όσες φορές χρειάζεται έτσι ώστε να οδηγεί σε βέβαια αποτελέσματα.

Η υπόθεση που επαληθεύτηκε με τη πειραματική διαδικασία μετατρέπεται σε νόμο και γίνεται γενίκευση του νόμου ως σύνολο νόμων ώστε να αποτελέσει μια θεωρία. Με τις διατυπωμένες θεωρίες είναι δυνατό οι φυσικοί επιστήμονες να προβλέπουν φυσικά φαινόμενα που μέχρι στιγμής δεν έχουν παρατηρηθεί.

Στον αρχαίο κόσμο οι φιλόσοφοι χρησιμοποιούσαν την παρατήρηση και έπειτα έκαναν λογικούς συλλογισμούς. Τον 4^ο π.Χ. αιώνα ο Αριστοτέλης έπειτα από μια σειρά παρατηρήσεων στην πτώση των σωμάτων έκανε το λογικό συλλογισμό ότι τα βαρύτερα σώματα πέφτουν πιο γρήγορα από τα ελαφρότερα.

Ο Γαλιλαίος προσπάθησε να επιβεβαιώσει ή να διαψεύσει τον ισχυρισμό του Αριστοτέλη, εγκαινιάζοντας για πρώτη φορά την επιστημονική μέθοδο, η οποία βασίζεται στην πειραματική διαδικασία. Πήρε τον ισχυρισμό του Αριστοτέλη ως υπόθεση και αναπαρήγαγε το φαινόμενο με τη μορφή πολλών πειραμάτων κάτω από ελεγχόμενες συνθήκες. Ως αποτέλεσμα είχε να διαψεύσει την άποψη του Αριστοτέλη και να απορρίψει την αρχική υπόθεση αφού βρήκε ότι τα σώματα έπεφταν σχεδόν ταυτόχρονα. Σύμφωνα με την παράδοση ο Γαλιλαίος άφηνε να πέσουν από τον κεκλιμένο πύργο της Πίζας σφαίρες διαφορετικού βάρους και οι μαθητές του παρατηρούσαν ότι έφταναν στο έδαφος σχεδόν ταυτόχρονα.

Ο Γαλιλαίος παρατήρησε ότι οι μικρές διαφορές στο χρόνο πτώσης οφείλεται στον αέρα που αντιστεκόταν στην πτώση των σωμάτων και μάλιστα όσο πιο μεγάλη επιφάνεια έχει το σώμα τόσο μεγαλύτερη ήταν η αντίσταση του αέρα. Ο Γαλιλαίος διατύπωσε νέα υπόθεση: Αν δεν υπάρχει αέρας, όλα τα σώματα ανεξάρτητα από το βάρος τους πέφτουν ταυτόχρονα στο έδαφος, όταν αφεθούν ταυτόχρονα από το ίδιο ύψος. Ο Γαλιλαίος κάνοντας πολλά πειράματα με κεκλιμένα επίπεδα με αυλάκια και κάνοντας προσεκτικές μετρήσεις της θέση και του χρόνου πτώσης των σωμάτων επιβεβαίωσε την υπόθεση του. Μάλιστα διατύπωσε τη σχέση που δίνει το ύψος με τον χρόνο. Αργότερα οι επιστήμονες ανακάλυψαν την αντλία κενού και έκαναν το πείραμα της πτώσης των σωμάτων σε συνθήκες κενού και επαλήθεψαν πανηγυρικά για ακόμη φορά την υπόθεση του Γαλιλαίου.

Μερικές δεκαετίες αργότερα, η υπόθεση του Γαλιλαίου εντάχθηκε σε μια γενικότερη θεωρία που διατύπωσε ο Νεύτωνας για τις κινήσεις των σωμάτων τόσο γήινων όσο και ουράνιων, αποτελώντας τους τρεις Νόμους του Νεύτωνα που είναι η βάση της Κλασικής Μηχανικής.

Η επιστημονική στάση

Στη σύγχρονη επιστήμη οι επιστήμονες δεν επιτρέπεται να είναι δογματικοί και είναι υποχρεωμένοι να ελέγχουν την ορθότητα των υποθέσεων τους με προσεκτικές παρατηρήσεις και επανειλημμένα πειράματα. Η αυθεντία, δηλαδή η πεποίθηση για την κατοχή της απόλυτης αλήθειας είναι ξένη προς την επιστημονική στάση. Αν αργότερα βρεθούν πειραματικά δεδομένα που αναιρούν μια θεωρία, οι επιστήμονες αναθεωρούν τους νόμους και τη θεωρία, έτσι ώστε να συμφωνούν με τα αποτελέσματα των πειραμάτων. Ο Αϊνστάιν έλεγε: «Απαιτούνται πολλά πειράματα για να βεβαιωθεί η θεωρία μου και μόνο ένα για να απορριφθεί»

Τα φυσικά μεγέθη και η μέτρηση τους

Ας εξετάσουμε το εξής φυσικό φαινόμενο: Μια μπάλα πέφτει από ψηλό κτίριο. Για να περιγράψουμε την πτώση της μπάλας χρησιμοποιούμε ποσοτικές έννοιες όπως «ύψος», «χρονική στιγμή», «ταχύτητα», «επιτάχυνση». Αυτές τις έννοιες ονομάζουμε φυσικά μεγέθη.

Ας επαναλάβουμε τον ορισμό: φυσικά μεγέθη είναι οι ποσοτικές έννοιες που μπορούν να μετρηθούν και χρησιμοποιούνται για την μελέτη καθώς και για την περιγραφή του φυσικού φαινομένου. Παραδείγματα φυσικών μεγεθών είναι το μήκος, το εμβαδόν, ο όγκος, ο χρόνος, η ταχύτητα, η μάζα, η πυκνότητα.

Η μέτρηση ενός φυσικού μεγέθους είναι η διαδικασία σύγκρισης του με άλλο ομοειδές μέγεθος που ονομάζεται μονάδα μέτρησης. Η τιμή που προκύπτει από τη μέτρηση του φυσικού μεγέθους ονομάζεται αριθμητική τιμή, ενώ η αριθμητική τιμή μαζί με τη μονάδα μέτρησης αποτελούν το μέτρο του φυσικού μεγέθους. Σύμφωνα με την επιστημονική μέθοδο, μετρώντας τα φυσικά μεγέθη μπορούμε να εκφράσουμε τις συσχετίσεις μεταξύ τους με μαθηματικούς τύπους-σχέσεις.

Μια μέτρηση μπορεί να είναι άμεση ή έμμεση. Άμεση μέτρηση έχουμε, για παράδειγμα, τη μέτρηση του πλάτους του θρανίου χρησιμοποιώντας ως μονάδα μέτρησης το μολύβι. Κατά τη μέτρηση βρίσκουμε το πλάτος του θρανίου να έχει μέτρο 12,5 μολύβια. Έμμεση μέτρηση είναι π.χ. εκείνη της μέτρησης της ταχύτητας του φωτός όπου χρησιμοποιούμε σύνθετες πειραματικές μεθόδους και μαθηματικά.

Κατά τη μέτρηση όσο κι αν δεν θέλουμε, υπεισέρχονται σφάλματα που μπορεί να οφείλονται είτε στην κατασκευή των οργάνων, είτε σε δικά μας λάθη κατά τη διάρκεια της μέτρησης είτε σε παράγοντες που δεν μπορούν να εντοπισθούν. Θα πρέπει να εκτιμούμε και να μειώνουμε τα σφάλματα στους υπολογισμούς μας, έτσι ώστε να παίρνουμε αξιόπιστα αποτελέσματα.

Κάποια φυσικά μεγέθη γίνονται άμεσα αντιληπτά με τις αισθήσεις μας και δεν χρειάζεται να ορισθούν με τη βοήθεια άλλων. Αυτά τα μεγέθη ονομάζονται θεμελιώδη και είναι (για τη μηχανική) το μήκος, ο χρόνος και η μάζα. Οι μονάδες μέτρησης των θεμελιωδών μεγεθών ορίζονται με τρόπο αυθαίρετο (βλέπε παρακάτω) και ονομάζονται θεμελιώδης μονάδες. Στο Διεθνές Σύστημα Μονάδων S.I. οι θεμελιώδης μονάδες της μηχανικής είναι οι εξής: για το μήκος είναι το μέτρο (m), για το χρόνο είναι το δευτερόλεπτο (s), ενώ για τη μάζα είναι το χιλιόγραμμο (Kg).

Μέτρηση του μήκους

Το μήκος είναι το θεμελιώδης φυσικό μέγεθος που χρησιμοποιούμε για να καθορίζουμε αποστάσεις. Στο Διεθνές Σύστημα Μονάδων, για τη μέτρηση του μήκους, χρησιμοποιούμε ως μονάδα μέτρησης το μέτρο που συμβολίζεται με το λατινικό γράμμα m. Το 1791 το μέτρο ορίστηκε αυθαίρετα ως το 1/10.000.000 της απόστασης του Βόρειου Πόλου από τον Ισημερινό της Γης. Προκειμένου το ένα μέτρο να είναι προσιτό και να είναι πιο εύχρηστος ο ορισμός του, το 1927 κατασκευάστηκε το πρότυπο μέτρο που είναι φτιαγμένο από ιριδιούχο λευκόχρυσο. Πάνω σ΄ αυτό χαράχθηκαν δυο γραμμές που η μεταξύ τους απόσταση ορίστηκε ως ένα μέτρο. Η ράβδος του πρότυπου μέτρου φυλάσσεται στο Μουσείο Μέτρων και Σταθμών στις Σέρβες της Γαλλίας.

Αργότερα χρειάστηκε να οριστεί το μέτρο με πολύ μεγαλύτερη ακρίβεια και το 1960 δόθηκε νέος ορισμός βασιζόμενος στο μήκος κύματος της ακτινοβολίας του ραδιενεργού ισοτόπου κρυπτον-86. Σήμερα, η μονάδα μέτρησης του μήκους 1m ορίζεται ως το διάστημα που διανύει το φως στο κενό σε χρονικό διάστημα ίσο με το κλάσμα 1/299.792.458 του δευτερολέπτου. Όργανα μέτρησης του μήκους είναι το υποδεκάμετρο, το πτυσσόμενο μέτρο και η μετροταινία.

Επειδή θέλουμε να μετράμε μήκη πολύ μεγαλύτερα ή πολύ μικρότερα του μέτρου, γι’ αυτό χρησιμοποιούμε πολλαπλάσια και υποπολλαπλάσια του μέτρου. Πολλαπλάσιο του μέτρου είναι το χιλιόμετρο Km.
Χιλιόμετρο km,    1km=1000m=10³m

Υποπολλαπλάσια του μέτρου είναι το εκατοστό cm και το χιλιοστό mm
Εκατοστό cm,  1cm = 1/100m = 10^-2m
Χιλιοστό mm,   1mm = 1/1000m = 10^-3m

Μέτρηση του χρόνου

Ο χρόνος είναι το θεμελιώδης φυσικό μέγεθος που μας βοηθά να καθορίζουμε την αλληλουχία των φυσικών γεγονότων. Για τη μέτρηση του χρόνου χρησιμοποιούμε περιοδικά φαινόμενα, δηλαδή εκείνα που επαναλαμβάνονται σε ίσα χρονικά διαστήματα με τον ίδιο ακριβώς τρόπο. Για παράδειγμα, περιοδικά φαινόμενα είναι η κίνηση του εκκρεμούς, η περιστροφή της Γης γύρω από τον άξονα της, κ.ά.  Στο διεθνές σύστημα μονάδων, η μονάδα μέτρησης του χρόνου, ορίζεται με τρόπο αυθαίρετο και είναι το δευτερόλεπτο που συμβολίζεται με το λατινικό γράμμα s. Αρχικά το δευτερόλεπτο ορίστηκε ως το κλάσμα 1/(24Χ60Χ60)=1/86400 της μέσης ηλιακής μέρας. Επειδή δεν μπορεί να οριστεί με απόλυτο τρόπο η μέση ηλιακή μέρα, το 1967 δόθηκε ο ακριβής ορισμός του δευτερολέπτου. Το ένα δευτερόλεπτο είναι ίσο με τη διάρκεια 9.162.631.770 περιόδων της ακτινοβολίας που εκπέμπεται κατά τη μετάπτωση μεταξύ δυο υπέρλεπτων επιπέδων της βασικής κατάστασης του ατόμου του καισίου 133. Όργανα μέτρησης του χρόνου είναι τα χρονόμετρα.

Υποδιαιρέσεις του δευτερόλεπτου είναι το μιλισεκοντ ms και το μικροσεκοντ μs
1ms = 1/1000s = 10^-3s
1μs = 1/1.000.000s = 10^-6s

Πολλαπλάσια του δευτερολέπτου είναι το λεπτό min και η ώρα h
1min = 60s
1h = 60min = 3.600s

Μέτρηση της μάζας

Η μάζα είναι το θεμελιώδης φυσικό μέγεθος που μας βοηθά να καθορίσουμε την ποσότητα της ύλης που έχει ένα σώμα και είναι ένα μέτρο της αδράνειας του. Θεωρούμε ότι όλα τα μικροσκοπικά σωματίδια που αποτελούνται τα άτομα (πρωτόνια, νετρόνια, ηλεκτρόνια) είναι φτιαγμένα από την ίδια ουσία την ύλη και συνεπώς όλα τα μακροσκοπικά σώματα θεωρούμε ότι είναι από ύλη, που ποσοτικά μπορεί να εκφραστεί από το φυσικό μέγεθος της μάζας.

Η αδράνεια ενός σώματος εκφράζει πόσο εύκολα ή δύσκολα μπορεί να τεθεί σε κίνηση ή να σταματήσει ένα σώμα και συνδέει τη μάζα με την κίνηση. Όσο μεγαλύτερη είναι η μάζα του σώματος τόσο πιο δύσκολα αλλάζει η κινητική κατάσταση του. Για παράδειγμα ένα άδειο μπουκάλι (μικρή μάζα) μπορεί να τεθεί ευκολότερα σε κίνηση με ένα σπρώξιμο, παρά ένα γεμάτο με νερό μπουκάλι (μεγάλη μάζα).

Στο Διεθνές Σύστημα μονάδων θεμελιώδης μονάδα μάζας είναι το χιλιόγραμμο. Αρχικά το 1889 το ένα χιλιόγραμμο ορίστηκε ίσο με τη μάζα του πρότυπου χιλιόγραμμου, ενός κυλίνδρου από ιριδιούχο λευκόχρυσο ο οποίος φυλάσσεται στο Μουσείο Μέτρων και Σταθμών στις Σέρβες της Γαλλίας.

Υποπολλαπλάσια του χιλιόγραμμου είναι το γραμμάριο g και το μιλιγραμάριο mg
1g = 1/1000Kg = 10^-3Kg
1mg = 1/1.000.000Kg = 10^-6Kg

Πολλαπλάσια του χιλιόγραμμου είναι ο τόνος tn
1tn = 1000Kg = 10³Kg

Για τη μέτρηση της μάζας χρησιμοποιείται ο ζυγός που βασίζεται στο βάρος των σωμάτων. Η μάζα ενός σώματος δεν πρέπει να συγχέεται με το βάρος του. Η μάζα ενός σώματος έχει την ίδια τιμή παντού στο σύμπαν όπου μπορεί να βρεθεί. Το βάρος είναι η δύναμη που έλκει το σώμα η Γη, που εξαρτάται από τον τόπο και το ύψος. Ισχύει η σχέση B=mg όπου Β είναι το βάρος και m είναι η μάζα, ενώ g είναι η επιτάχυνση της βαρύτητας που παίρνει διαφορετικές τιμές ανάλογα τον τόπο και το ύψος που αναφερόμαστε. Όμως η επιτάχυνση της βαρύτητας είναι σταθερή σε μικρά ύψη πάνω από την επιφάνεια της γης και έτσι με βάσει αυτό τον τύπο μπορούμε να μετράμε τη μάζα με αρκετά μεγάλη ακρίβεια.

Παράγωγα μεγέθη

Τα υπόλοιπα φυσικά μεγέθη πέρα από τα θεμελιώδη, μπορούν να ορισθούν με τη βοήθεια απλών μαθηματικών σχέσεων από τα θεμελιώδη, τα οποία ονομάζονται παράγωγα μεγέθη. Παραδείγματα παράγωγων μεγεθών είναι η ταχύτητα και η πυκνότητα. Η ταχύτητα ορίζεται από τα θεμελιώδη μεγέθη μήκος και χρόνος σαν το πηλίκο μήκος δια χρόνο. Η πυκνότητα ορίζεται από τα θεμελιώδη μεγέθη μάζα και μήκος σαν το πηλίκο μάζα δια όγκο ή σαν μάζα δια μήκος στην τρίτη δύναμη. Με τις ίδιες μαθηματικές σχέσεις που ορίζονται τα παράγωγα μεγέθη μπορούν να ορισθούν και οι μονάδες των παραγώγων μεγεθών βασισμένες στις μονάδες των θεμελιωδών μεγεθών.

Μέτρηση εμβαδόν

Εμβαδόν είναι το παράγωγο μέγεθος που χρησιμοποιείται για να καθορίσουμε την έκταση μιας επιφάνειας και ορίζεται από το θεμελιώδης μέγεθος του μήκους από τη σχέση:
Εμβαδόν τετραγώνου = μήκος πλευράς Χ μήκος πλευράς.
Μονάδα μέτρησης του εμβαδού είναι το τετραγωνικό μέτρο και εκφράζεται από την θεμελιώδης μονάδα του μήκους σαν (τετραγωνικό μέτρο):  1m X 1m = 1m²

Αν η επιφάνεια ορίζεται από κάποιο από τα κανονικά γεωμετρικά σχήματα, το εμβαδόν μπορεί να υπολογιστεί βάσει συγκεκριμένων γεωμετρικών τύπων. Έτσι το εμβαδόν ενός ορθογωνίου παραλληλογράμμου δίνεται από τον τύπο Ε = μήκος Χ πλάτος, το εμβαδόν ενός τριγώνου δίνεται από τον τύπο Ε = ½ βάση Χ ύψος  ενώ το εμβαδόν ενός κύκλου δίνεται από τον τύπο Ε=π(ακτίνα)²

Μέτρηση όγκου

Όγκος είναι το παράγωγο μέγεθος που χρησιμοποιείται για να καθορίσουμε το χώρο που καταλαμβάνει ένα αντικείμενο και ορίζεται από το θεμελιώδες μέγεθος του μήκους από τη σχέση:
Όγκος κύβου=μήκος ακμής Χ μήκος ακμής Χ μήκος ακμής
Μονάδα μέτρησης του όγκου είναι το κυβικό μέτρο και εκφράζεται από την θεμελιώδη μονάδα του μήκους σαν: (κυβικό μέτρο):  1m X 1m X 1m = 1m³
Αν το αντικείμενο έχει κανονικό γεωμετρικό σχήμα, ο όγκος του μπορεί να υπολογιστεί βάσει γεωμετρικών τύπων. Έτσι ο όγκος του ορθογωνίου παραλληλεπιπέδου, δίνεται από τον τύπο V = μήκος Χ πλάτος Χ ύψος. Ο όγκος κυλίνδρου δίνεται από τον τύπο V=π(ακτίνα)² Χ ύψος, ενώ ο όγκος της σφαίρας δίνεται από τον τύπο V=4/3π(ακτίνα)³

Μέτρηση της πυκνότητας

Για να απαντήσουμε στο ερώτημα πιο είναι πιο βαρύ ο σίδηρος ή το ξύλο, πρέπει να συγκρίνουμε τις μάζες σωμάτων που έχουν τον ίδιο όγκο. Καταλαβαίνουμε ότι ορίζεται ένα νέο φυσικό μέγεθος που καθορίζει τη μάζα του υλικού σε μια μονάδα όγκου. Έτσι βλέπουμε ότι η πυκνότητα εκφράζει πόσο πυκνό σε ύλη είναι το σώμα του συγκεκριμένου υλικού.

Η πυκνότητα έχει νόημα να οριστεί σε ομογενή σώματα φτιαγμένα από συγκεκριμένο υλικό και χαρακτηρίζει το υλικό καθαυτό όπως το σίδηρο, το ξύλο, το χαρτί κ.ά. Η πυκνότητα ενός υλικού ορίζεται με τον εξής τρόπο: Παίρνουμε ένα σώμα από αυτό το υλικό και μετράμε τη μάζα και τον όγκο του.

Η πυκνότητα ρ του υλικού του σώματος ορίζεται από το πηλίκο:
ρ = μάζα /όγκο = m / V

Η πυκνότητα είναι ανεξάρτητη από τον όγκο του σώματος που παίρνουμε, δηλαδή όποιο σώμα του αυτού υλικού σε οποιαδήποτε μέγεθος η παραπάνω σχέση δίνει την ίδια τιμή της πυκνότητας του υλικού. Μονάδα μέτρησης της πυκνότητας στο Διεθνές Σύστημα μονάδων S.I. είναι το 1Kg/m³. Πιο πρακτικές μονάδες είναι το 1g/cm³ και το 1Kg/L.

Παραδείγματα είναι ο σίδηρος που έχει πυκνότητα 7,8g/cm³ ενώ ο μόλυβδος Pb έχει πυκνότητα 11,4g/cm³. Αν συγκρίνουμε αυτές με τις πυκνότητες του λαδιού 0,9g/cm³ και του οινοπνεύματος 0,79g/cm³ μπορούμε να ισχυριστούμε ότι αυτά τα μέταλλα είναι πολύ βαρύτερα από τα παραπάνω υγρά.

Διεθνές Σύστημα μονάδων

Από την εποχή της Γαλλικής Επανάστασης οι άνθρωποι έκαναν προσπάθειες να καθιερωθεί ένα κοινό παγκόσμιας κλίμακας σύνολο μονάδων που θα εξυπηρετεί την εύκολη επικοινωνία των επιστημόνων. Τελικά το έτος 1960 καθιερώθηκε και πήρε την τελική μορφή το Διεθνές Σύστημα μονάδων S.I. Τα θεμελιώδη μεγέθη αυτού του συστήματος είναι το μήκος, η μάζα και ο χρόνος με τις αντίστοιχες θεμελιώδης μονάδες το μέτρο 1m, το χιλιόγραμμο 1Kg και το δευτερόλεπτο s. Στο Διεθνές Σύστημα μονάδων, θεμελιώδης μεγέθη είναι και η θερμοκρασία, η ένταση του ηλεκτρικού ρεύματος, η ένταση της ακτινοβολίας και η ποσότητα της ύλης με αντίστοιχες θεμελιώδης μονάδες το 1Κ (Κέλβιν), το 1Α (Αμπέρ), το 1cd (καντέλα) και το 1mol (γραμμομόριο).

Ένα άλλο σύστημα μονάδων που προτιμούν ορισμένοι επιστήμονες διότι οδηγεί σε κοινές μονάδες του ηλεκτρικού πεδίου και της μαγνητικής επαγωγής είναι το CGS, με θεμελιώδης μεγέθη το μήκος, τη μάζα και το χρόνο με θεμελιώδη μονάδες το εκατοστό cm, το γραμμάριο g και το δευτερόλεπτο s αντίστοιχα.

Πολλαπλάσια και υποπολλαπλάσια

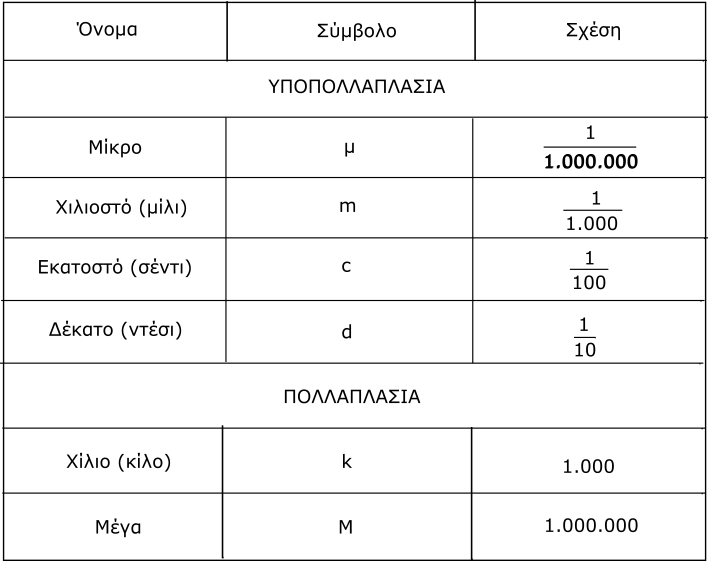
Πολλές φορές, όταν μετράμε ποσότητες χρησιμοποιώντας συγκεκριμένες μονάδες, όπως εκείνες του Διεθνές Συστήματος S.I. , η αριθμητική τιμή που προκύπτει μπορεί να είναι πολύ μεγάλη ή πολύ μικρή. Σε αυτές τις περιπτώσεις μπορούμε να χρησιμοποιήσουμε πολλαπλάσια και υποπολλαπλάσια των μονάδων μέτρησης οι οποίες εκφράζονται ως δυνάμεις του δέκα ή με γράμματα. Στον πίνακα που ακολουθεί αναγράφονται τα κυριότερα πολλαπλάσια και υποπολλαπλάσια που χρησιμοποιούνται ως πρόθεμα, σε όλες τις μονάδες των φυσικών μεγεθών.