Όλοι γνωρίζουμε ότι μια ηλεκτρική συσκευή, η οποία είναι συνδεμένη σε ένα ηλεκτρικό κύκλωμα, διαρρέεται από ηλεκτρικό ρεύμα. Δίνουμε τον ακόλουθο ορισμό: Κάθε συσκευή η οποία έχει δυο άκρα ή πόλους, με τους οποίους συνδέεται σε ένα ηλεκτρικό κύκλωμα, ονομάζεται ηλεκτρικό δίπολο. Ηλεκτρικά δίπολα είναι ο λαμπτήρας, ο ηλεκτρικός κινητήρας κ.ά. Ένα ηλεκτρικό δίπολο, μετατρέπει την ηλεκτρική ενέργεια σε άλλη μορφή ενέργειας.

Όταν εφαρμόσουμε τάση V στα άκρα ενός διπόλου, θα διαρρέεται από ρεύμα έντασης Ι. Αν αλλάξουμε την τιμή της τάσης που εφαρμόζουμε στα άκρα ενός ηλεκτρικού διπόλου, θα αλλάξει και η τιμή του ρεύματος που το διαρρέει. Ο τρόπος με τον οποίο μεταβάλλεται η τιμή της έντασης του ηλεκτρικού ρεύματος καθώς μεταβάλλουμε την τάση στα άκρα του, εξαρτάται από τη φύση του ηλεκτρικού διπόλου.

Στην πειραματική διάταξη του σχήματος, παρατηρείται μεταβολή της έντασης του ρεύματος σε σχέση με τη μεταβολή της τάσης που εφαρμόζεται σε ένα λαμπτήρα και σε ένα ηλεκτρικό κινητήρα. Αν τριπλασιάσουμε την τάση στα άκρα του λαμπτήρα, το ρεύμα που τον διαρρέει σχεδόν τριπλασιάζεται και αν τριπλασιάσουμε την τάση στα άκρα ενός ηλεκτρικού κινητήρα το ρεύμα διπλασιάζεται.

Αντίσταση του διπόλου

Για να συσχετίσουμε την τάση που εφαρμόζεται στους πόλους ενός ηλεκτρικού διπόλου, με το ρεύμα που προκαλεί ή τάση, ορίζουμε ένα νέο φυσικό μέγεθος που το ονομάζουμε ηλεκτρική αντίσταση του διπόλου και το συμβολίζουμε με το γράμμα R.

Ηλεκτρική αντίσταση ενός ηλεκτρικού διπόλου, ονομάζεται το πηλίκο της ηλεκτρικής τάσης V που εφαρμόζεται στους πόλους του ηλεκτρικού διπόλου, προς την ένταση Ι του ηλεκτρικού ρεύματος που το διαρρέει.

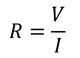
Η αντίσταση είναι παράγωγο μέγεθος. Η μονάδα αντίστασης στο Διεθνές Σύστημα Μονάδων είναι το 1Ωμ (1Ohm) που εκφράζεται ως

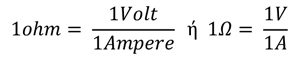
1 Ωμ είναι η αντίσταση ενός ηλεκτρικού διπόλου, που όταν εφαρμόσουμε τάση 1 V στα άκρα του, διαρρέεται από ρεύμα τιμής 1Α

Στην ηλεκτρολογία και στην ηλεκτρονική χρησιμοποιούνται πολλαπλάσια του Ωμ, τα οποία είναι τα εξής:

1ΚΩ (κίλο-ωμ) =10³Ω και 1ΜΩ (μέγα-ωμ) = 10⁶Ω

Για τη μέτρηση της αντίστασης ενός ηλεκτρικού διπόλου, χρησιμοποιούνται όργανα που ονομάζονται ωμόμετρα. Τα πολύμετρα ενσωματώνουν πολλά όργανα σε μια μονάδα, που εκτός από ωμόμετρα (μέτρηση αντίστασης) είναι βολτόμετρα (μέτρηση τάσης) και αμπερόμετρα (μετράνε ρεύμα).

Γενικά για ένα ηλεκτρικό δίπολο, η αντίσταση του μεταβάλλεται με την τάση που εφαρμόζουμε στα άκρα του. Υπάρχει μια κατηγορία ηλεκτρικών διπόλων, που ονομάζονται αντιστάτες, για τα οποία η αντίσταση τους είναι σταθερή ανεξάρτητη της τάσης που εφαρμόζουμε στα άκρα τους και της έντασης που τα διαρρέει. Σε αυτή την κατηγορία ηλεκτρικών διπόλων με σταθερή αντίσταση ανήκουν οι απλοί μεταλλικοί αγωγοί.

Νόμος του Ωμ

Το πιο απλό ηλεκτρικό δίπολο είναι ένας μεταλλικός αγωγός, δηλ. ένα μεταλλικό σύρμα. Για να μελετήσουμε τη σχέση τάσης – έντασης ρεύματος ενός μεταλλικού αγωγού εκτελούμε το ακόλουθο πείραμα:

Με ένα τροφοδοτικό μεταβλητής τάσης εφαρμόζουμε ηλεκτρική τάση στα άκρα ενός μεταλλικού αγωγού, ενώ με ένα βολτόμετρο συνδεμένο παράλληλα στα άκρα του αγωγού, μετράμε την ηλεκτρική τάση στα άκρα του και με ένα αμπερόμετρο συνδεμένο σε σειρά με τον αγωγό, μετράμε την ένταση του ρεύματος που τον διαρρέει.

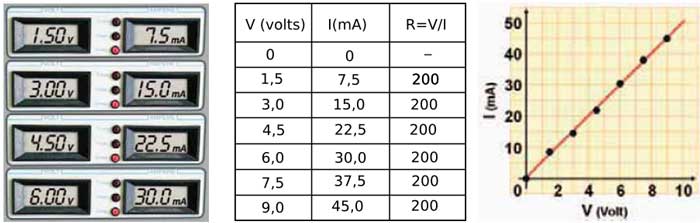
Για διάφορες ηλεκτρικές τάσεις στα άκρα του αγωγού, μετράμε την ένταση του ρεύματος που τον διαρρέει και καταγράφουμε τα αποτελέσματα των μετρήσεων στον παραπάνω πίνακα. Στην τρίτη στήλη υπολογίζουμε το πηλίκο της ηλεκτρικής τάσης προς την αντίστοιχη ένταση του ρεύματος και καταγράφουμε την αντίσταση του αγωγού.

Από τα δεδομένα του πίνακα ηλεκτρικής τάσης – έντασης ρεύματος, κατασκευάζουμε το διάγραμμα της έντασης του ηλεκτρικού ρεύματος, στον κατακόρυφο άξονα, σε συνάρτηση με την εφαρμοζόμενη ηλεκτρική τάση στον αγωγό, στον οριζόντιο άξονα. Παρατηρούμε ότι το διάγραμμα (γραφική παράσταση) είναι ευθεία γραμμή, που διέρχεται από την αρχή των αξόνων. Συμπεραίνουμε ότι τα δυο μεγέθη η ηλεκτρική τάση στα άκρα του αγωγού και η ένταση του ρεύματος που τον διαρρέει είναι ανάλογα δηλαδή ο λόγος τους είναι σταθερός. Το ίδιο προκύπτει και από την τρίτη στήλη του πίνακα, που υπολογίσαμε το λόγο της ηλεκτρικής τάσης προς την ένταση του ρεύματος V/I και έχουν την ίδια τιμή. Συμπέρασμα: η αντίσταση R του μεταλλικού αγωγού είναι σταθερή ανεξάρτητη της τάσης που εφαρμόζεται στα άκρα του.

Ο γερμανός φυσικός Ωμ (Ohm), γενίκευσε τα αποτελέσματα παρόμοιων πειραμάτων και διατύπωσε ένα νόμο για να εκφράσει την σχέση μεταξύ της ηλεκτρικής τάσης που εφαρμόζεται σε ένα μεταλλικό αγωγό, με την ένταση του ρεύματος που προκαλεί.

Η ένταση Ι του ηλεκτρικού ρεύματος που διαρρέει ένα μεταλλικό αγωγό, είναι ανάλογη της διαφοράς δυναμικού V που εφαρμόζεται στα άκρα του.

Σύμφωνα με το νόμο του Ωμ, η αντίσταση ενός μεταλλικού αγωγού είναι ανεξάρτητη της ηλεκτρικής τάσης που εφαρμόζεται στα άκρα του και της έντασης του ηλεκτρικού ρεύματος που τον διαρρέει. Δηλαδή:

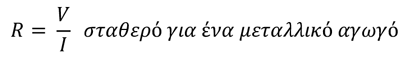
Από αυτή τη σχέση προκύπτει ότι: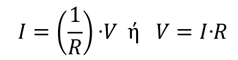

Δηλαδή η ένταση Ι του ρεύματος που διαρρέει ένα αγωγό, είναι ανάλογη της ηλεκτρικής τάσης V που εφαρμόζεται στα άκρα του αγωγού με σταθερά αναλογίας το 1/R

Η γραφική παράσταση της σχέσης 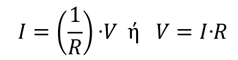είναι ευθεία γραμμή που διέρχεται από το μηδέν.

Ο νόμος του Ωμ εφαρμόζεται σε μια κατηγορία ηλεκτρικών διπόλων, ενώ υπάρχουν ηλεκτρικά δίπολα όπως η κρυσταλλοδίοδος, το τρανζίστορ, η ηλεκτρονική λυχνία που συναντάμε στις ηλεκτρονικές συσκευές, όπως επίσης ο λαμπτήρας νέον, ο ηλεκτρικός κινητήρας κ.ά. τα οποία αν και διαρρέονται από ρεύμα δεν ακολουθούν το νόμο του Ωμ, δηλαδή η εφαρμοζόμενη τάση προκαλεί ηλεκτρικό ρεύμα του οποίου η ένταση δεν είναι ανάλογη της ηλεκτρικής τάσης που εφαρμόζεται στα άκρα τους και συνεπώς η αντίσταση τους μεταβάλλεται με την ηλεκτρική τάση.

Αντίθετα, οι μεταλλικοί αγωγοί με την προϋπόθεση ότι διατηρούμε τη θερμοκρασία σταθερή, συμπεριφέρονται σύμφωνα με το νόμο του Ωμ και η αντίσταση τους είναι σταθερή ανεξάρτητα της εφαρμοζόμενης τάσης στα άκρα τους.

Κάθε ηλεκτρικό δίπολο το οποίο ικανοποιεί το νόμο του Ωμ, χαρακτηρίζεται ως αντιστάτης. Οι αντιστάτες έχουν την ιδιότητα να μετατρέπουν εξ ολοκλήρου την ηλεκτρική ενέργεια σε θερμική.

Νόμος του Ωμ και μικρόκοσμος

Σύμφωνα με το νόμο του Ωμ, η ένταση του ρεύματος που διαρρέει ένα μεταλλικό αγωγό, είναι ανάλογη της ηλεκτρικής τάσης που εφαρμόζεται στα άκρα του. Αυξάνοντας την ηλεκτρική τάση στα άκρα του αγωγού, τα ελεύθερα ηλεκτρόνια αποκτούν μεγαλύτερη ενέργεια και άρα μεγαλύτερη ταχύτητα. Όσο αυξάνεται η ταχύτητα των ηλεκτρονίων τόσο μεγαλύτερος αριθμός ηλεκτρονίων περνά από μια διατομή του αγωγού, σε ορισμένο χρόνο και άρα τόσο μεγαλύτερη θα είναι η ένταση του ρεύματος που διαρρέει τον αγωγό.

Μικροσκοπική ερμηνεία της αντίστασης ενός μεταλλικού αγωγού

Παίρνουμε δυο αντιστάτες με διαφορετική αντίσταση και στα άκρα τους εφαρμόζουμε την ίδια ηλεκτρική τάση (αίτιο). Σύμφωνα με το νόμο του Ωμ, από τον αντιστάτη με τη μεγαλύτερη αντίσταση θα διαρρέεται από μικρότερης έντασης ηλεκτρικού ρεύματος (αποτέλεσμα) από ότι από τον αντιστάτη με την μικρότερη αντίσταση. Έτσι από τον αντιστάτη με τη μεγαλύτερη αντίσταση, θα διέρχεται μικρότερος αριθμός ηλεκτρονίων στο ίδιο χρονικό διάστημα. Τα ηλεκτρόνια δυσκολεύονται να κινούνται στον αντιστάτη με την μεγαλύτερη αντίσταση.

Επομένως, η αντίσταση ενός αγωγού (αντιστάτη) εκφράζει το μέτρο της δυσκολίας που προβάλλει ο αγωγός στη διέλευση του ρεύματος μέσα από αυτόν.

Για να ερμηνεύσουμε τη δυσκολία διέλευσης του ηλεκτρικού ρεύματος από ένα μεταλλικό αγωγό (αντιστάτη), θα ανατρέξουμε στη μικροσκοπική περιγραφή του μεταλλικού αγωγού και του ηλεκτρικού ρεύματος.

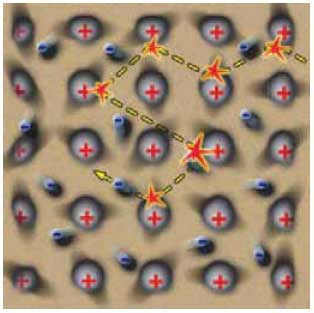
Καθώς εφαρμόζουμε ηλεκτρική τάση στα άκρα του μεταλλικού αγωγού, δημιουργείται ηλεκτρικό πεδίο στο εσωτερικό του, με αποτέλεσμα να ασκούνται ηλεκτρικές δυνάμεις στα ελεύθερα ηλεκτρόνια του μεταλλικού αγωγού και έτσι εκτελούν προσανατολισμένη κίνηση με αυξανόμενη ταχύτητα.

Όμως κατά την κίνηση τους τα ελεύθερα ηλεκτρόνια συγκρούονται με τα ιόντα του μετάλλου και σε κάθε σύγκρουση χάνουν μέρος της κινητικής ενέργειας, η οποία μεταφέρεται στα ιόντα και έτσι η ταχύτητα τους μειώνεται. Αμέσως μετά τη σύγκρουση, η δύναμη του ηλεκτρικού πεδίου προκαλεί εκ νέου αύξηση της ταχύτητας των κινούμενων ηλεκτρονίων μέχρι την επόμενη σύγκρουση, οπότε επαναλαμβάνεται η ίδια διαδικασία.

Η αντίσταση ενός μεταλλικού αγωγού στη διέλευση του ηλεκτρικού ρεύματος μέσα από αυτόν οφείλεται στις συγκρούσεις των ελεύθερων ηλεκτρονίων με τα ιόντα του μετάλλου.

Παράγοντες από τους οποίους εξαρτάται η αντίσταση ενός αγωγού

Με την ενασχόληση μας με τον ηλεκτρισμό, προκύπτει το ερώτημα: από ποιους παράγοντες εξαρτάται η αντίσταση ενός μεταλλικού αγωγού; Για να απαντήσουμε, θα ακολουθήσουμε τη διαδικασία της επιστημονικής μεθόδου: Πρώτα κάνουμε υποθέσεις και έπειτα καταφεύγουμε στο πείραμα για να δούμε αν οι υποθέσεις μας είναι σωστές ή όχι. Ξεκινούμε με την υπόθεση ότι η αντίσταση ενός αγωγού εξαρτάται από το υλικό του μεταλλικού αγωγού, τις διαστάσεις του (μήκος και διατομή) και από την θερμοκρασία του.

Στην πειραματική διαδικασία μετράμε με ένα ωμόμετρο την αντίσταση διαφόρων μεταλλικών αγωγών, μεταβάλλοντας κάθε φορά έναν από τους παράγοντες της υπόθεσης και διατηρούμε τους υπόλοιπους σταθερούς.

Εξάρτηση από το μήκος Παίρνουμε μεταλλικούς αγωγούς, με μήκος ακέραιο πολλαπλάσιο ενός αρχικού μήκους, του ίδιου υλικού και της ίδιας διατομής και με ένα ωμόμετρο μετράμε την αντίσταση τους. Βρίσκουμε ότι α) Ο αγωγός μήκους l₁ έχει αντίσταση R₁ β) Ο αγωγός μήκους l₂=2l₁ έχει αντίσταση R₂ = 2R₁ γ) Ο αγωγός μήκους l₃=3l₁ έχει αντίσταση R₃ = 3R₁ . Δηλαδή οι αγωγοί με διπλάσιο ή τριπλάσιο μήκος, έχουν διπλάσια ή τριπλάσια αντίσταση αντίστοιχα.

Η αντίσταση ενός σύρματος είναι ανάλογη του μήκους του

Συμπέρασμα: η αντίσταση R ενός μεταλλικού αγωγού σταθερής διατομής είναι ανάλογη του μήκους του.

Εξάρτηση από το εμβαδόν διατομής Παίρνουμε μεταλλικούς αγωγούς διαφορετικού εμβαδού διατομής, με εμβαδόν διατομής ακέραιο πολλαπλάσιο ενός αρχικού εμβαδού διατομής, του ίδιου υλικού και του ίδιου μήκους και με ένα ωμόμετρο μετράμε την αντίσταση τους. Βρίσκουμε ότι α) Ο αγωγός με εμβαδόν διατομής Α₁ έχει αντίσταση R₁ β) Ο αγωγός με εμβαδόν διατομής Α₂ = 2Α₁ έχει αντίσταση R₂=R₁/2 γ) Ο αγωγός με εμβαδόν διατομής Α₃=3Α₁ έχει αντίσταση R₃ = R₁/3 . Δηλαδή ο αγωγός με διπλάσια διατομή έχει τη μισή αντίσταση και ο αγωγός με την τριπλάσια διατομή έχει υποτριπλάσια αντίσταση.

Συμπέρασμα: η αντίσταση R ενός μεταλλικού αγωγού σταθερού μήκους είναι αντιστρόφως ανάλογη του εμβαδού Α της διατομής του.

Εξάρτηση από το είδος του υλικού Παίρνουμε μεταλλικούς αγωγούς από διαφορετικά υλικά, που έχουν το ίδιο μήκος και το ίδιο εμβαδόν διατομής και με ένα ωμόμετρο μετράμε την αντίσταση τους. Διαπιστώνουμε ότι η αντίσταση των μεταλλικών αγωγών είναι διαφορετική.

Συμπέρασμα: η αντίσταση R ενός μεταλλικού αγωγού εξαρτάται από το είδος του υλικού από τον οποίο είναι κατασκευασμένος.

Εξάρτηση από τη θερμοκρασία Με ένα ωμόμετρο μετράμε την αντίσταση ενός μεταλλικού αγωγού που βρίσκεται σε ένα λαμπτήρα πυράκτωσης. Μελετάμε τη μεταβολή της αντίστασης του μεταλλικού αγωγού στον λαμπτήρα, σε συνάρτηση με τη θερμοκρασία του, καθώς ο λαμπτήρας είναι βυθισμένος σε δοχείο με νερό, το οποίο θερμαίνουμε και με ένα θερμόμετρο μετράμε τη θερμοκρασία του.

Με επεξεργασία των πειραματικών δεδομένων, συμπεραίνουμε ότι η αντίσταση του μεταλλικού αγωγού αυξάνεται με την αύξηση της θερμοκρασίας.

Γενικό συμπέρασμα

Μελετώντας τα δεδομένα των πειραμάτων που παρουσιάσαμε προηγουμένως, συμπεραίνουμε ότι η αντίσταση ενός μεταλλικού αγωγού, σταθερής διατομής σε όλο το μήκος του:
α] είναι ανάλογη του μήκος του (l)
β] είναι αντιστρόφως ανάλογη του εμβαδού (Α) της διατομής του
γ] εξαρτάται από το είδος του υλικού που είναι κατασκευασμένος ο μεταλλικός αγωγός
δ] εξαρτάται από την θερμοκρασία του αγωγού.

Τα παραπάνω συμπεράσματα μπορούν να εκφραστούν με τη μαθηματική σχέση:

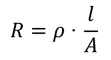
όπου R είναι η αντίσταση του αγωγού, Α το εμβαδόν της διατομής του και l το μήκος του. Ο συντελεστής αναλογίας (ρ) είναι χαρακτηριστικό του υλικού που είναι κατασκευασμένος ο αγωγός και ονομάζεται ειδική αντίσταση του υλικού, το οποίο έχει ως μονάδα μέτρησης το Ω·m

Όσο μικρότερη ειδική αντίσταση ρ έχει το υλικό, τόσο καλύτερος αγωγός του ηλεκτρικού ρεύματος είναι. Για παράδειγμα, σε θερμοκρασία 20^οC μετρήθηκε η ειδική αντίσταση του χαλκού και του αλουμινίου και βρέθηκε ότι η ειδική αντίσταση του χαλκού είναι μικρότερη από εκείνη του αλουμινίου. Επομένως ο χαλκός είναι καλύτερος αγωγός του ηλεκτρικού ρεύματος από το αλουμίνιο.

Η τιμή της ειδικής αντίστασης εξαρτάται από τη θερμοκρασία του αγωγού. Αυξάνεται καθώς αυξάνεται η θερμοκρασία του. Για περιοχή θερμοκρασιών έως τους 100^oC, η αύξηση της ειδικής αντίστασης δίνεται από τη σχέση:

ρ_θ = ρ₀·(1+α·θ)

όπου ρ_θ η ειδική αντίσταση του υλικού σε θερμοκρασία θ βαθμούς Κελσίου, ενώ ρ₀ η ειδική αντίσταση του υλικού στους μηδέν βαθμούς Κελσίου. Ο παράγοντας α ονομάζεται θερμικός συντελεστής ειδικής αντίστασης, που για τα περισσότερα καθαρά μέταλλα έχει την τιμή 1/(273⁰C)

Υπάρχουν μεταλλικοί αγωγοί κατασκευασμένοι από ορισμένα κράματα για τα οποία η ειδική αντίσταση είναι ανεξάρτητη από τη θερμοκρασία τους. Τέτοια υλικά είναι όπως η κονσταντάνη (κράμα χαλκού και νικελίου). Αυτά τα υλικά έχουν μηδενικό συντελεστή ειδικής αντίστασης (α=0). Για τον ίδιο λόγο, τα υλικά αυτά χρησιμοποιούνται για την κατασκευή εξαρτημάτων ηλεκτρικών οργάνων ακριβείας, για τα οποία η λειτουργία τους δεν πρέπει να επηρεάζεται με τις μεταβολές της θερμοκρασίας.

Η ειδική αντίσταση των ημιαγωγών ελαττώνεται με την αύξηση της θερμοκρασίας, δηλαδή οι ημιαγωγοί έχουν αρνητικό θερμικό συντελεστή ειδικής αντίστασης (α<0).

Επειδή η ειδική αντίσταση ενός υλικού αυξάνεται με τη θερμοκρασία, συμπεραίνουμε ότι η αντίσταση ενός μεταλλικού αγωγού (σύρμα) αυξάνεται με τη θερμοκρασία, σύμφωνα με τη σχέση:

R_θ = R₀·(1+α·θ)

όπου R_θ η αντίσταση του αγωγού στους θ βαθμούς Κελσίου και R₀ η αντίσταση του αγωγού στους μηδέν βαθμούς Κελσίου (0^οC).

Πως ερμηνεύεται η εξάρτηση της αντίστασης από την θερμοκρασίας; Για να ερμηνεύσουμε την αύξηση της αντίστασης ενός μεταλλικού αγωγού με την αύξηση της θερμοκρασίας, θα καταφύγουμε στο μικρόκοσμο, στην ατομική δομή της ύλης.

Η αντίσταση ενός μεταλλικού αγωγού προέρχεται από τις συγκρούσεις των ελεύθερων ηλεκτρονίων με τα ιόντα του μετάλλου, τα οποία ταλαντώνονται γύρω από τις θέσεις ισορροπίας τους. Καθώς αυξάνεται η θερμοκρασία του μεταλλικού αγωγού, οι κινήσεις των ιόντων γίνονται πιο έντονες, με αποτέλεσμα να αυξάνεται το πλάτος της ταλάντωσης τους και οι συγκρούσεις με τα ελεύθερα ηλεκτρόνια να είναι πιο συχνές. Έτσι με την αύξηση της θερμοκρασίας του αγωγού, αυξάνεται το πλήθος των συγκρούσεων και επομένως την αύξηση της αντίστασης του μεταλλικού αγωγού.

Μεταβλητός αντιστάτης

Ο μεταβλητός αντιστάτης είναι ένας αντιστάτης του οποίου μπορούμε να αλλάξουμε την αντίσταση του μετακινώντας ένα δρομέα ή περιστρέφοντας ένα κουμπί. Τη μεταβλητή αντίσταση αφού την συνδέσουμε κατάλληλα, τη χρησιμοποιήσουμε για να ρυθμίσουμε την ένταση του ρεύματος που διαρρέει μια συσκευή, που σε αυτή την περίπτωση λέγεται ροοστάτης ή χρησιμοποιείται για να ρυθμίσουμε την τάση στα άκρα μιας συσκευής, που στη περίπτωση αυτή λέγεται ποτενσιόμετρο.

Πως λειτουργεί ένας ροοστάτης Ένας ροοστάτης αποτελείται από ένα αγωγό (σύρμα) μεγάλου μήκους, τυλιγμένος γύρω από ένα μονωτικό κύλινδρο. Κατά μήκος της επιφάνειας του κυλίνδρου μπορεί και μετακινείται ένας μεταλλικός δρομέας με μονωτική χειρολαβή, ο οποίος βρίσκεται σε αγώγιμη επαφή με τον αγωγό. Με μετακίνηση του δρομέα, αυξάνεται ή μειώνεται το μήκος του αγωγού το οποίο διαρρέεται από ηλεκτρικό ρεύμα. Έτσι η λειτουργία του ροοστάτη βασίζεται στην εξάρτηση της αντίστασης του αγωγού από το μήκος του.

Πως εξηγείται η λειτουργία του ροοστάτη; Κατασκευάζουμε το κύκλωμα του σχήματος, όπου ένας ροοστάτης συνδέεται σε σειρά με ένα λαμπτήρα και με τους πόλους μιας ηλεκτρικής πηγής. Το ηλεκτρικό ρεύμα διαρρέει τον αγωγό του ροοστάτη μόνο στο τμήμα ΑΔ. Μετακινώντας το δρομέα προς το άκρο Β, το μήκος του αγωγού που διαρρέεται από ηλεκτρικό ρεύμα αυξάνει, με αποτέλεσμα να αυξάνει η αντίσταση του και αυτό για το λόγο ότι τα δυο αυτά μεγέθη είναι ανάλογα.

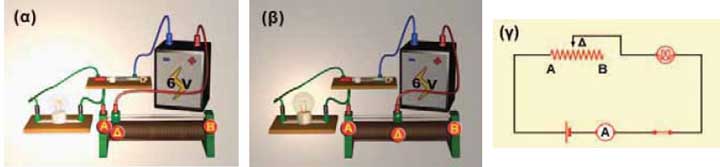
Σύμφωνα με το νόμο του Ωμ, η ένταση του ηλεκτρικού ρεύματος σε ένα αγωγό, συνδέεται με την τάση στα άκρα του από τη σχέση:

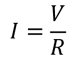
Για την ηλεκτρική πηγή που συνδέεται ο ροοστάτης, διατηρώντας την τάση της σταθερή, με αύξηση της αντίστασης στο ροοστάτη μειώνεται η ένταση του ηλεκτρικού ρεύματος και έτσι η φωτοβολία του λαμπτήρα μειώνεται. Όταν μετακινήσουμε το δρομέα του ροοστάτη προς το άκρο Α, η αντίσταση του ροοστάτη μειώνεται, με αποτέλεσμα την αύξηση της έντασης του ηλεκτρικού ρεύματος, που οδηγεί στην αύξηση της φωτοβολίας του λαμπτήρα.

Πως λειτουργεί το ποτενσιόμετρο Στο σχήμα φαίνεται πως συνδέεται μια μεταβλητή αντίσταση, ώστε να λειτουργεί σαν ποτενσιόμετρο. Στο κύκλωμα αυτό, τα δυο άκρα του ποτενσιόμετρου συνδέονται με τους πόλους μιας σταθερής ηλεκτρικής πηγής. Παίρνουμε την επιθυμητή τάση από το άκρο Α και το άκρο του δρομέα Δ, η οποία είναι ένα κλάσμα της τάσης της ηλεκτρικής πηγής. Στα άκρα αυτά συνδέουμε μια συσκευή που θέλουμε να τροφοδοτήσουμε με τάση.

Με ένα ποτενσιόμετρο μπορούμε να αλλάξουμε την ένταση του ήχου σε ένα ραδιόφωνο ή στερεοφωνικό συγκρότημα.

Πως το ποτενσιόμετρο διαιρεί την τάση Στο ίδιο κύκλωμα (βλέπε σχήμα) μετακινώντας το δρομέα του ποτενσιομέτρου, αυξάνουμε το μήκος του και επομένως την αντίσταση R_ΑΔ μεταξύ του άκρου Α και του άκρου του δρομέα Δ. Σύμφωνα με το νόμο του Ωμ, η τάση V μεταξύ των Α και Δ είναι ανάλογη με την R_ΑΔ

V_ΑΔ = I·R_ΑΔ

Έτσι αν συνδέσουμε μια συσκευή μεταξύ των άκρων Α και Δ από την οποία να διαρρέεται από ρεύμα μικρής έντασης, τότε αυτή η τάση V_ΑΔ εφαρμόζεται στα άκρα της συσκευής η οποία μεταβάλλεται καθώς μετακινούμε το δρομέα του ποτενσιομέτρου.