Κίνηση στο μακρόκοσμο όσο στο μικρόκοσμο

Αν κοιτάξουμε γύρω μας, βλέπουμε ότι τα πάντα κινούνται. Η κίνηση εμφανίζεται παντού, στο μικρόκοσμο και στον μακρόκοσμο. Στον μικρόκοσμο σε σώματα μικρά που δεν μπορούμε να δούμε, όπως τα ηλεκτρόνια κινούνται μέσα στα μέταλλα, τα άτομα και τα μόρια ταλαντεύονται μέσα στα σώματα. Οι κινήσεις στο μικρόκοσμο γίνονται αντιληπτές από τα αποτελέσματα τους, π.χ. το ηλεκτρικό ρεύμα και τη θερμοκρασία. Στον μακρόκοσμο με το σύνολο των ουράνιων σωμάτων, οι κινήσεις φαίνονται αντιληπτές καθώς οι πλανήτες περιστρέφονται γύρω από τον Ήλιο και οι γαλαξίες απομακρύνονται ο ένας από τον άλλο κ.ά. Έτσι βγάζουμε το συμπέρασμα ότι η κίνηση είναι χαρακτηριστική ιδιότητα της ύλης και εμφανίζεται παντού, από τους μακρινούς γαλαξίες μέχρι το εσωτερικό των μικροσκοπικών ατόμων.

Λέμε ότι ένα σώμα κινείται όταν αλλάζει θέση ως προς ένα άλλο σώμα αναφοράς που το θεωρούμε ως παρατηρητή. Η κίνηση ενός σώματος είναι σχετική και ορίζεται ανάλογα ως προς ένα παρατηρητή. Έτσι ένας παρατηρητής βλέπει την κίνηση ενός αντικειμένου με τον δικό του τρόπο. Είναι δυνατόν να έχουμε περισσότερους από ένα παρατηρητές που να βλέπουν την κίνηση, ο καθένας με τον δικό του χαρακτηριστηκό τρόπο. Π.χ. ο οδηγός ενός αυτοκινήτου βλέπει τον συνεπιβάτη του ακίνητο, ενώ ένας άνδρας στο δρόμο βλέπει το ίδιο άτομο να κινείται με την ταχύτητα του αυτοκινήτου. Συνεπώς η κίνηση ενός αντικειμένου έχει σχέση και εκδηλώνεται διαφορετικά ανάλογα με τον παρατηρητή.  Έτσι σωστά λέμε ότι η κίνηση είναι φαινόμενο σχετικό.

Στη φυσική χρειαζόμαστε ακριβή τρόπο περιγραφής της κίνησης και γι’ αυτό χρησιμοποιούμε τη γλώσσα των μαθηματικών. Τα φυσικά μεγέθη (π.χ. θέση, μετατόπιση, ταχύτητα) παριστάνονται με σύμβολα και εκφράζουμε τις σχέσεις μεταξύ τους με μαθηματικές εξισώσεις και χρησιμοποιούμε γραφικές παραστάσεις (διαγράμματα) για να δείξουμε πως τα φυσικά μεγέθη μεταβάλλονται με το χρόνο.

Για να κάνουμε πιο απλή τη μελέτη της κίνησης, σε αυτό το κεφάλαιο, υιοθετούμε τις παρακάτω παραδοχές. Πρώτο. Ασχολούμαστε με την κίνηση του σώματος χωρίς να μας ενδιαφέρει η αιτία που την προκαλεί (τι είναι αυτό που κάνει το σώμα να κινείται). Ο κλάδος της Φυσικής που ασχολείται με την κίνηση, χωρίς να ασχολείται με τα αίτια της, ονομάζεται Κινηματική. Δεύτερο. Πρώτα μελετάμε τις ευθύγραμμες κινήσεις. Ευθύγραμμη είναι η κίνηση που γίνεται σε ευθεία γραμμή. Τρίτο. Μελετάμε την κίνηση των σωμάτων, χωρίς να παίρνουμε υπόψη τις διαστάσεις τους, δηλαδή τα αντιμετωπίζουμε ως υλικά σημεία. Υλικό σημείο θεωρείται ένα σώμα που έχει μάζα αλλά οι διαστάσεις του είναι πολύ μικρές σε σχέση με τις διαστάσεις που χρησιμοποιούμε για να περιγράψουμε την κίνηση του. Παράδειγμα: Όταν μελετάμε την κίνηση της Γης γύρω από τον Ήλιο, επειδή η ακτίνα της Γης είναι πολύ μικρότερη από την απόσταση της από τον Ήλιο, την θεωρούμε ως υλικό σημείο. Επίσης όταν ένα σώμα κάνει μεταφορική κίνηση, που όλα τα σημεία του σώματος μετατοπίζονται το ίδιο, μπορούμε να το θεωρήσουμε το ίδιο ως υλικό σημείο, με ίση μάζα στο κέντρο μάζας του ή σε κάποιο άλλο σημείο του.

Προσδιορισμός της θέσης σώματος στην ευθεία

Πως προσδιορίζεται η θέση σώματος στην ευθεία

Θεωρούμε την ευθύγραμμη κίνηση, για παράδειγμα την κίνηση ενός αυτοκινήτου πάνω σε ευθύγραμμο δρόμο. Τίθεται το ερώτημα: πως μπορούμε να προσδιορίσουμε τη θέση του αυτοκινήτου σε κάποια χρονική στιγμή;

Για να απαντήσουμε, πρέπει πρώτα να ορίσουμε ένα σύστημα αναφοράς πάνω στην ευθεία που ορίζεται με την την ευθύγραμμη κίνηση του σώματος. Επιλέγουμε αυθαίρετα ένα σημείο πάνω στην ευθεία ως σημείο αναφοράς, π.χ. τη θέση του σήματος της τροχαίας και προσαρμόζουμε νοητά μια κλίμακα (μετροταινία) πάνω στην ευθεία της κίνησης, με το μηδέν πάνω στο σημείο αναφοράς. Κατά σύμβαση θεωρούμε τις θέσεις δεξιά του σημείου αναφοράς ως «θετικές», ενώ τις θέσεις αριστερά του σημείου αναφοράς ως «αρνητικές». Τώρα λέμε ότι έχουμε ορίσει ένα σύστημα αναφοράς πάνω στην ευθεία.

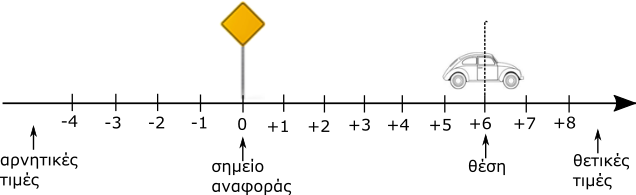
Η θέση του αντικειμένου πάνω στην ευθεία στην οποία έχουμε ορίσει ένα σύστημα αναφοράς, ορίζεται σαν την απόσταση του αντικειμένου από το σημείο αναφοράς με θετικό πρόσημο αν βρίσκεται στις θετικές θέσεις και με αρνητικό πρόσημο αν βρίσκεται στις αρνητικές θέσεις.

Στο παράδειγμα του παρακάτω σχήματος, το αυτοκίνητο, το οποίο θεωρούμε ως υλικό σημείο με ίση μάζα στο μέσο του, όπως κάνουμε και στο ποδήλατο, βρίσκεται 6 μέτρα δεξιά του σημείου αναφοράς επομένως η θέση του είναι x_A=+6m ενώ ο ποδηλάτης βρίσκεται 3 μέτρα αριστερά του σημείου αναφοράς, επομένως η θέση του είναι x_P=-3m.

Ως απόσταση δυο σημείων Α και Β ορίζουμε το μήκος του ευθύγραμμου τμήματος που έχει ως άκρα αυτά τα σημεία. Για δυο σημεία πάνω σε ένα σύστημα αναφοράς στην ευθεία, η απόσταση τους βρίσκεται με την αφαίρεση της μικρότερης θέσης από την μεγαλύτερη θέση.

Για παράδειγμα στο παρακάτω σχήμα, αν η θέση του σημείου Α είναι x_A=+7m και η θέση του σημείου Β είναι x_B=+3m τότε η απόσταση μεταξύ των Α και Β είναι:

d_AB=x_A-x_B=7m-3m=4m

Αν η θέση του σημείου Γ είναι x_Γ=-4m τότε η απόσταση μεταξύ των σημείων Γ και Β είναι:

d_ΓΒ=x_B-x_Γ=3m-(-4m)=7m

Η απόσταση δυο σημείων είναι πάντα θετικός αριθμός και δεν δείχνει πιο σημείο είναι δεξιά και πιο είναι αριστερά. Η απόσταση είναι μήκος, άρα προσδιορίζεται πλήρως από ένα θετικό αριθμό και τη μονάδα μέτρησης που αποτελούν το μέτρο της.

Μονόμετρα και διανυσματικά μεγέθη

Κάποια μεγέθη, όπως για παράδειγμα ο όγκος, προσδιορίζονται πλήρως με την αριθμητική τιμή του και τη μονάδα μέτρησης. Π.χ. αν πούμε ότι ο όγκος του βιβλίου είναι 700cm³ αντιλαμβανόμαστε πλήρως το μέγεθος του. Μονόμετρα ονομάζονται εκείνα τα μεγέθη που προσδιορίζονται πλήρως από το μέτρο τους δηλαδή από ένα αριθμό και τη μονάδα μέτρησης τους. Μονόμετρα είναι, για παράδειγμα, το μήκος (π.χ. λέμε ότι το πλάτος του βιβλίου είναι L=15cm), η πυκνότητα (π.χ. λέμε ότι η πυκνότητα του σιδήρου είναι ρ=7,8g/cm³) η μάζα (π.χ. λέμε ότι η μάζα του θρανίου είναι m=30Kg).

Υπάρχουν και μεγέθη που η γνώση του μέτρου τους δεν αρκεί για τον πλήρη προσδιορισμό τους. Για παράδειγμα η θέση, η οποία για τον πλήρη προσδιορισμό της δεν αρκεί μόνο το μέτρο της αλλά χρειάζεται η επιπρόσθετη πληροφορία της κατεύθυνσης ως προς την οποία βρίσκεται το σώμα σε σχέση με το σημείο αναφοράς. Διανυσματικά ονομάζονται τα μεγέθη εκείνα που για τον πλήρη προσδιορισμό τους απαιτείται να ξέρουμε το μέτρο τους αλλά και την κατεύθυνση τους.

Τα διανυσματικά μεγέθη παριστάνονται με τη μαθηματική έννοια του διανύσματος. Διάνυσμα είναι ένα ευθύγραμμο τμήμα, όπου το ένα άκρο του το έχουμε ονομάσει ως αρχή και το άλλο του ως τέλος. Δηλαδή θεωρούμε το διάνυσμα σαν ένα βέλος.

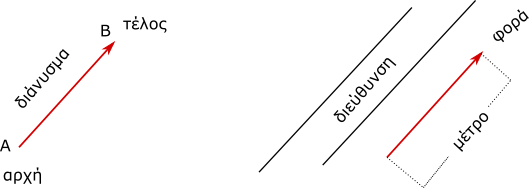
Κάθε διάνυσμα έχει ως στοιχεία του το μέτρο, την διεύθυνση και τη φορά. Το μήκος του διανύσματος (σε κατάλληλη κλίμακα) δίνει το μέτρο του διανυσματικού μεγέθους. Η ευθεία στην οποία βρίσκεται το διάνυσμα και κάθε παράλληλη της, παριστάνει την διεύθυνση του διανυσματικού μεγέθους. Η αιχμή του διανύσματος παριστάνει την φορά του διανυσματικού μεγέθους. Η διεύθυνση και η φορά μαζί δίνουν την κατεύθυνση του διανυσματικού μεγέθους.

Δύο διανύσματα είναι ίσα αν έχουν ίσα μέτρα, την ίδια διεύθυνση και την ίδια φορά. Τα ίσα διανύσματα περιγράφουν το ίδιο διανυσματικό μέγεθος, δηλαδή αν μετακινήσουμε ένα διάνυσμα παράλληλα στον εαυτόν του διατηρώντας το μήκος του διατηρεί τις ίδιες «πληροφορίες»

Χρονική στιγμή

Για να μελετήσουμε την κίνηση εκτός από την μετροταινία χρειαζόμαστε και ένα χρονόμετρο. Κάθε ένδειξη του χρονομέτρου αντιπροσωπεύει και μια χρονική στιγμή. Η χρονική στιγμή μας δείχνει πότε ένα κινούμενο αντικείμενο βρίσκεται σε κάποια συγκεκριμένη θέση. Η χρονική στιγμή μηδέν t=0 είναι η στιγμή που το χρονόμετρο αρχίζει να μετρά το χρόνο.

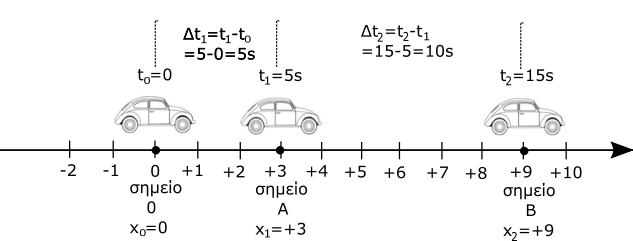
Στο παράδειγμα του παραπάνω σχήματος το αυτοκίνητο τη χρονική στιγμή μηδέν t₀=0 περνά από το σημείο αναφοράς 0, ενώ τη χρονική στιγμή t₁=5s περνά από τη θέση Α με x₁=+3  ενώ τη χρονική στιγμή t₂=15s περνά από τη θέση Β με x₂=+9 Το χρονικό διάστημα συμβολίζεται με Δt και απαντά στο ερώτημα πόσο διαρκεί το φαινόμενο. Το χρονικό διάστημα είναι η διαφορά δυο χρονικών στιγμών. Έτσι στο παράδειγμα μας, η κίνηση από το σημείο αναφοράς 0 έως τη θέση Α διαρκεί Δt₁ = t₁-0 = 5-0 = 5s , ενώ από τη θέση Α στη θέση Β η κίνηση διαρκεί Δt₂= t₂-t₁ = 15-5 = 10s

Μετατόπιση

Μετατόπιση λέμε την μεταβολή της θέσης ενός αντικειμένου. Αν ένα αντικείμενο μετατοπίζεται από τη θέση Α₁ στη θέση Α₂ , η μετατόπιση του αντικειμένου ορίζεται με το διάνυσμα , το οποίο έχει αρχή το σημείο Α₁ και τέλος το σημείο Α₂. Αν η θέση Α₁ έχει (διάνυσμα) θέσης  και η θέση Α₂ έχει (διάνυσμα) θέσης ,  η μετατόπιση από τη θέση Α₁ έως την Α₂ ορίζεται ως το διάνυσμα    και είναι ανεξάρτητη από τον τρόπο που κινήθηκε από την θέση  ως την θέση .

Στις ευθύγραμμες κινήσεις η διεύθυνση των διανυσμάτων είναι σταθερή και μάλιστα είναι παράλληλη στην ευθεία της κίνησης. Σε αυτή την περίπτωση, τη φορά των διανυσμάτων τη δηλώνουμε με θετικό πρόσημο (+) αν το διάνυσμα έχει κατεύθυνση προς τα θετικά και αρνητικό πρόσημο (-) αν το διάνυσμα έχει κατεύθυνση προς τα αρνητικά.

Στις ευθύγραμμες κινήσεις που όλα τα διανύσματα έχουν την ίδια διεύθυνση, αντί για τα διανύσματα γράφουμε την αλγεβρική τους τιμή. Η αλγεβρική τιμή ενός διανύσματος στην κίνηση πάνω σε ευθεία είναι το μέτρο του διανύσματος με θετικό πρόσημο αν έχει την θετική φορά και με αρνητικό πρόσημο αν έχει την αρνητική φορά.

Σαν διάνυσμα θέσης ενός σώματος στην κίνηση πάνω σε ευθεία, είναι εκείνο το διάνυσμα που έχει ως αρχή το σημείο αναφοράς και τέλος την θέση του σώματος. Σύμφωνα με τον ορισμό που δώσαμε παραπάνω, η θέση του σώματος στην κίνηση πάνω σε ευθεία είναι η αλγεβρική τιμή του διανύσματος της θέσης του.

Στην ευθύγραμμη κίνηση η μετατόπιση από τη θέση x_A (σημείο Α) στη θέση x_B (σημείο Β) είναι ίση με την διαφορά: Δx = x_B – x_A

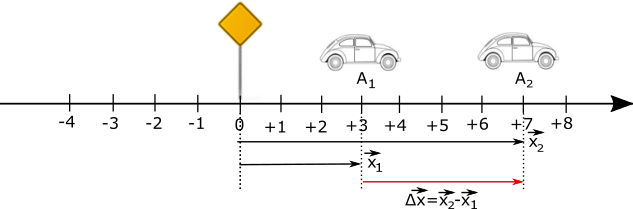
Παράδειγμα. Στο παρακάτω σχήμα φαίνονται δυο θέσης ενός κινούμενου οχήματος και η μετατόπιση του.

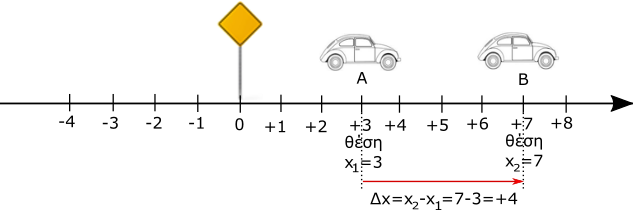
Σε κάποια χρονική στιγμή το όχημα βρίσκεται στο σημείο Α, η θέση του οποίου είναι x₁=3  ενώ σε κατοπινή χρονική στιγμή βρίσκεται στο σημείο Β, η θέση του οποίου  είναι x₂=7 . Η μετατόπιση του από τη θέση Α στη θέση Β είναι Δx=x₂-x₁= 7-3 = +4 που έχει θετική τιμή που σημαίνει ότι η κίνηση γίνεται προς τα θετικά.

Όμοια για το παρακάτω σχήμα:

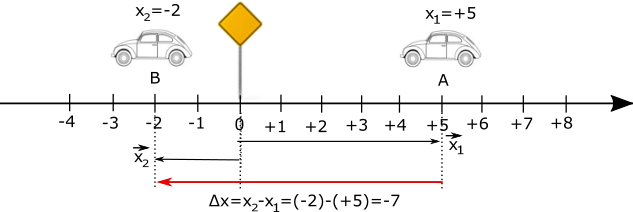
Το όχημα στη αρχική θέση x₁=+5 έχει διάνυσμα θέσης  και στην κατοπινή θέση x₂=-2 έχει διάνυσμα θέσης , η μετατόπιση του από τη θέση  στη θέση  είναι  που γραφικά σχεδιάζεται όπως φαίνεται στο παραπάνω σχήμα όπου βλέπουμε ότι έχει την αρνητική κατεύθυνση. Με αριθμητικό τρόπο η μετατόπιση είναι Δx=x₂-x₁= (-2)-(+5) = -7 που έχει αρνητικό πρόσημο που σημαίνει ότι η μετατόπιση έχει την αρνητική φορά.

Τροχιά

Καθώς ένα σώμα κινείται αλλάζει διαρκώς θέση. Η γραμμή που σχηματίζεται από το σύνολο των διαδοχικών θέσεων από τις οποίες περνά το σώμα κατά την κίνηση του ονομάζεται τροχιά. Ανάλογα με τη μορφή της τροχιάς, η κίνηση λέγεται ευθύγραμμη αν η τροχιά του είναι ευθεία γραμμή, ενώ λέγεται καμπυλόγραμμη αν η τροχιά του είναι καμπύλη. Παράδειγμα καμπυλόγραμμης κίνησης είναι η κυκλική κίνηση.